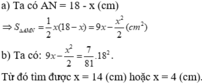Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AM=x; AN=y
MN^2=AM^2+AN^2
=>\(MN=\sqrt{x^2+y^2}\)
\(P_{AMN}=AM+AN+MN=x+y+\sqrt{x^2+y^2}=2a\)
và x+y>=2*căn xy; \(\sqrt{x^2+y^2}>=\sqrt{2xy}\)
=>\(2a=x+y+\sqrt{x^2+y^2}>=2\sqrt{xy}+\sqrt{2xy}\)
=>\(2a>=\sqrt{xy}\left(2+\sqrt{2}\right)\)
=>\(\sqrt{xy}< =\dfrac{2a}{2+\sqrt{2}}\)
=>\(S_{AMN}=\dfrac{1}{2}xy< =\dfrac{1}{2}\cdot\left(\dfrac{2a}{2+\sqrt{2}}\right)^2=\left(3-2\sqrt{2}\right)a^2\)
Dấu = xảy ra khi \(x=y=\left(2-\sqrt{2}\right)a\)

Phương ơi làm được chưa. Em chưa làm được. Bài này hình như làm rồi nhưng không nhớ :<
(Hân)
Chị cx chưa làm đc , mỗi ý a là làm đc thui .
Bài này đúng là làm rùi nhưng lúc đấy chị cx chưa bít làm và cô cx ko có chữa. Vậy nên giờ làm lại cx ko bít làm !!!!

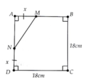
Xét tam giác ADB có : M là trung điểm của AB(gt)
N là trung điểm của AD(gt)
=> MN là đường trung bình của tam giác ADB ( đ/n)
=> MN//DB và MN =1/2 DB ( t/c)
Xét tam giác AMN và tam giác ABD có : MN // BD ( cmt)
tam giác AMN đồng dạng với tam giác ABD ( hq đ/y ta lét) => SAMN/SABD=(1/2)^2=1/4 (1)
Xét tam giác ABD và tam giác CDBcó
AB=CD( ABCD là hbh )
góc A = góc C (nt)
AD=cb(nt)
=> tam giác ABD = tam giác CDB (cgc)
=> tam giác ABD đồng dạng tam giác CDB(t/c)
=> tam giác ABD=1/2 HBh ABCD(2)
Từ 1 2 => SAMN/SABCD=1/8
Vẽ AH⊥BC⊥BC cắt MN tại H'
Ta có : AH'=HH'=12AH12AH(vì MN là trung điểm => AH′=12AHAH′=12AH)
Lại có:
SABC=12.AH.BC=60cm2SABC=12.AH.BC=60cm2 và SAMN=12AH′.MNSAMN=12AH′.MN.Mà
MN là đường trung bình của tam giác ABC=>MN=12BCMN=12BC
=>SAMN=12.12AH.12BC=14(12AH.BC)=12.60=15(cm2)SAMN=12.12AH.12BC=14(12AH.BC)=12.60=15(cm2)
Vậy SAMN=15cm2

Bài 1:
a) Đặt \(6x+7=y\)
\(PT\Leftrightarrow y^2\left(y-1\right)\left(y+1\right)=72\)
\(\Leftrightarrow y^4-y^2-72=0\)
\(\Leftrightarrow\left(y^2-9\right)\left(y^2+8\right)=0\)
Mà \(y^2+8>0\left(\forall y\right)\)
\(\Rightarrow y^2-9=0\Leftrightarrow\left(y-3\right)\left(y+3\right)=0\Leftrightarrow\left(6x+4\right)\left(6x+10\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}6x+4=0\\6x+10=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{2}{3}\\x=-\frac{5}{3}\end{cases}}\)
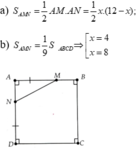
b) đk: \(x\ne\left\{-4;-5;-6;-7\right\}\)
\(PT\Leftrightarrow\frac{1}{\left(x+4\right)\left(x+5\right)}+\frac{1}{\left(x+5\right)\left(x+6\right)}+\frac{1}{\left(x+6\right)\left(x+7\right)}=\frac{1}{18}\)
\(\Leftrightarrow\frac{1}{x+4}-\frac{1}{x+5}+\frac{1}{x+5}-\frac{1}{x+6}+\frac{1}{x+6}-\frac{1}{x+7}=\frac{1}{18}\)
\(\Leftrightarrow\frac{1}{x+4}-\frac{1}{x+7}=\frac{1}{18}\)
\(\Leftrightarrow\frac{3}{\left(x+4\right)\left(x+7\right)}=\frac{1}{18}\)
\(\Leftrightarrow x^2+11x+28=54\)
\(\Leftrightarrow x^2+11x-26=0\)
\(\Leftrightarrow\left(x+13\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-13\\x=2\end{cases}}\)
Bài 2 không tiện vẽ hình nên thôi nhờ godd khác:)
Bài 3:
Ta có:
\(a_n=1+2+3+...+n\)
\(a_{n+1}=1+2+3+...+n+\left(n+1\right)\)
\(\Rightarrow a_n+a_{n+1}=2\cdot\left(1+2+3+...+n\right)+\left(n+1\right)\)
\(=2\cdot\frac{n\left(n+1\right)}{2}+n+1\)
\(=n^2+n+n+1=\left(n+1\right)^2\)
Là SCP => đpcm