Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AM=x; AN=y
MN^2=AM^2+AN^2
=>\(MN=\sqrt{x^2+y^2}\)
\(P_{AMN}=AM+AN+MN=x+y+\sqrt{x^2+y^2}=2a\)
và x+y>=2*căn xy; \(\sqrt{x^2+y^2}>=\sqrt{2xy}\)
=>\(2a=x+y+\sqrt{x^2+y^2}>=2\sqrt{xy}+\sqrt{2xy}\)
=>\(2a>=\sqrt{xy}\left(2+\sqrt{2}\right)\)
=>\(\sqrt{xy}< =\dfrac{2a}{2+\sqrt{2}}\)
=>\(S_{AMN}=\dfrac{1}{2}xy< =\dfrac{1}{2}\cdot\left(\dfrac{2a}{2+\sqrt{2}}\right)^2=\left(3-2\sqrt{2}\right)a^2\)
Dấu = xảy ra khi \(x=y=\left(2-\sqrt{2}\right)a\)

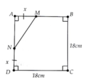
Có : \(S_{ABCD}=36cm^2\Rightarrow BC^2=36\Rightarrow BC=6cm\left(Vi:BC>0\right)\)
Vì ABCD là hình vuông (gt)
\(\Rightarrow BC=DC=AD=AB=6\left(cm\right)\)
Mà : M , N lần lượt là trung điểm của BC , CD
\(\Rightarrow BM=MC=DN=NC=\frac{BC}{2}=\frac{6}{2}=3\left(cm\right)\)
Có : \(S_{AMN}=S_{ABCD}-\left(S_{ADN}+S_{ABM}+S_{NMC}\right)\)
\(=36-\left(\frac{1}{2}.AD.DN+\frac{1}{2}.AB.BM+\frac{1}{2}.MC.NC\right)\)
\(=36-\left(\frac{1}{2}.6.3+\frac{1}{2}.6.3+\frac{1}{2}.3.3\right)=\frac{27}{2}\left(cm^2\right)\)
Chúc bạn học tốt !!!