Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
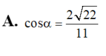
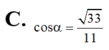
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
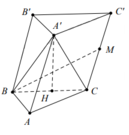
Ta có cos α = cos C C ' ; B M ^ = cos B M C ^ .
Cạnh A ' H = B C 3 2 = a 3 2 , A H = A B 3 2 = a 3 2
A A ' = A ' H 2 + A H 2 = a 6 2 ⇒ M C = a 6 4 .
Cạnh B ' H = A ' B ' 2 + A ' H 2 = a 7 2 .
Do đó cos B ' B H ^ = B B ' 2 + B H 2 - B ' H 2 2 B B ' . B H = 0 ⇒ B ' B ⊥ B H
⇒ M C ⊥ B C ⇒ c o s M B C ^ = M C B M = M C B C 2 + M C 2 = 33 11 .

Đáp án D
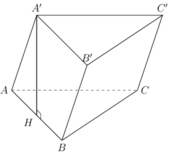
Ta có góc giữa cạnh bên AA' với mặt đáy (ABC) là:
góc A ' A H ^ và tan A ' A H = A ' H A H
Suy ra A ' H = a 2 . tan 30 ° = a 3 6
Do đó V = A ' H . S A B C = a 3 6 . a 2 3 4 = a 3 8
Đáp án D