Cho hai số phức z = a + b i và z ’ = a ’ + b ’ i (a,b,a’,b’ÎR) . Số phức zz’ có phần thực là
A. aa’ + bb’
B. ab’ – a’b
C. aa’ - bb’
D. ab’ + a’b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Có z . z ' = a a ' − b b ' + a b ' + a ' b i .
Vậy phần ảo là: a b ' + b a ' i .

\(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=\frac{ayz+bxz+cxy}{xyz}=0\Rightarrow ayz+bxz+cxy=0\)
\(\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)^2=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{xy}{ab}+\frac{xz}{ac}+\frac{yz}{bc}\right)\)
\(=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{cxy+bxz+ayz}{abc}\right)=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\cdot\frac{0}{abc}=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)^2\)mà \(\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)^2=1^2=1\)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\)

Chọn B.
Ta có: z = ( 2 + i) ( 3 - i) = 6 - 2i + 3i - i2 = 7 + i
Nên ![]() vậy phần thực bằng a = 7 và phần ảo b = -1.
vậy phần thực bằng a = 7 và phần ảo b = -1.

Chọn C.
Theo giả thiết ta có:
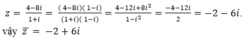
⇒ Phần thực a = -2 và phần ảo bằng b = 6.
Chọn C