Chứng minh các đẳng thức sau: a b + b a a b : 1 a - b = a - b v ớ i a , b d ư ơ n g , a ≠ b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
8 tháng 11 2019
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2021
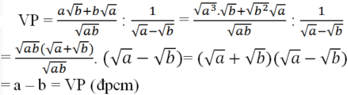
Biến đổi tương đương:
\(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+b^2+2ab\ge4ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
K
31 tháng 1 2019
Ta có:
Vế trái: -a.(c-d)-d.(a+c)
=-ac+ad-ad-cd
=-ac-cd (1)
Vế phải: -c(a+d)=-ac-cd (1)
Vì (1)=(2)
<=> -a.(c-d)-d.(a+c)=-c.(a+d) (đpcm)
(Lưu ý: "đpcm" nghĩa là "điều phải chứng minh".)
31 tháng 1 2019
Lời giải:
1) \(VT=-a.\left(c-d\right)-d.\left(a+c\right)\)
$=-ac+ad-da-dc$
$=-ac-dc$
$=-c(a+d) (đpcm)$
$2) (3a+2).(2a-1)+(3-a).(6a+2)-17.(a-1)$
$=6a^2-3a+4a-2+18a+6-6a^2-2a-17a+17$
$=21$
Vậy giá trị biểu thức không phụ thuộc vào a
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 7 2023
a/
\(a\left(b-c\right)-b\left(a+c\right)+c\left(a-b\right)=\)
\(=ab-ac-ab-bc+ac-bc=-2bc\)
b/
\(a\left(1-b\right)+a\left(a^2-1\right)=\)
\(=a-ab+a^3-a=a^3-ab=a\left(a^2-b\right)\)
c/
\(a\left(b-x\right)+x\left(a+b\right)=ab-ax+ax+bx=\)
\(=ab+bx=b\left(a+x\right)\)
VT
0
BN
4 tháng 7 2023
a, \(VT=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)=a-b=VP\) đpcm
b,\(VT=1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}-\dfrac{a^2-a}{a-1}=1-\sqrt{a}+\sqrt{a}-a=1-a=VP\) đpcm
DH
1
PP
2
NT
5 tháng 7 2016
a/ -(b-a)^3= -(b^3-3b^2a+3ba^2-a^3)
= -b^3+3ab^2a-3ba^2+a^3
= (a-b)^3
b/ tương tự ta dùng hằng đẳng thức để chứng minh
5 tháng 7 2016
a) a - b = - (b - a) = (-1)*(b - a)
=> (a - b)3 = [(-1)*(b - a)]3 = (-1)3 * (b - a)3 = -(b - a)3
b) -(a + b) = (- a - b)
=> (-1)2 * (a + b)2 = (-a - b)2
=> (-a -b)2 = (a + b)2
E
3
9 tháng 7 2019
a) (a-b)^3=-(b-a)^3
\(Taco:-\left(b-a\right)^3\)
=\(-\left(b-a\right)\left(b-a\right)\left(b-a\right)\)
\(=\left(a-b\right)\left(b-a\right)\left(b-a\right)\)
\(=-\left(a-b\right)\left(a-b\right)\left(b-a\right)\)
\(=\left(a-b\right)\left(a-b\right)\left(a-b\right)=\left(a-b\right)^3\)
9 tháng 7 2019
\(\left(-a-b\right)^2=\left(-a-b\right)\left(-a-b\right)\)
\(=-\left(a+b\right)\left(-a-b\right)\)
\(=\left(a+b\right)\left(a+b\right)\)
\(=\left(a+b\right)^2\)