Phương trình z 2 + a z + b = 0 nhận z = 1 - 2i làm nghiệm. Khi đó a + b bằng
A. 3
B. 4
C. 5
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
A. z=a+bi hoặc z=-a-bi (loại)
B. ![]() (loại)
(loại)
C. giải phương trình bậc hai ẩn z có nghiệm z=a+bi; z=a-bi (thỏa mãn)

Thay z = 1 + i vào phương trình đã cho ta có:
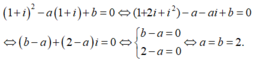
Chọn đáp án B.

\(\Delta'=4-5=-1\Rightarrow\left[{}\begin{matrix}z_1=2+i\\z_2=2-i\end{matrix}\right.\)
\(\Rightarrow\left(z_1-1\right)^{2019}+\left(z_2-1\right)^{2019}=\left(i+1\right)^{2019}+\left(i-1\right)^{2019}\)
\(=\left(i+1\right)\left[\left(i+1\right)^2\right]^{1009}+\left(i-1\right)\left[\left(i-1\right)^2\right]^{1009}\)
\(=\left(i+1\right)\left(2i\right)^{1009}+\left(1-i\right)\left(-2i\right)^{1009}=\left(2i\right)^{1009}\left(i+1+i-1\right)=\left(2i\right)^{1009}.2i=\left(2i\right)^{1010}=-2^{1010}\)
=>D
P/s: Sry nó bị trôi thông báo nên toi ko để ý

Cho phương trình: X2 - (2m4+1)x + m2 + m - 1 = 0
a. Giải phương trình khi m=1 khi đó lập một phương trình nhận t1 = x1 + x2 và t2 = x1 x2 làm nghiệm.
b. Chứng minh phương trình có nghiệm với mọi m.
c. Tìm m sao cho:
A=(2x1 - x2)(2x2 - x1) đạt GTNN, thín GTNN đó (giá trị nhỏ nhất).
chịu @_@
a) thay m=1 vào lập denta giải pt ra đc x1=(3+căn5)/2;x2=(3-căn5)/2
t1=x1+x2=(3+căn5)/2+(3-căn5)/2=3
t2=x1*x2=(3+căn5)/2*(3-căn5)/2=1
=>t1+t2=4;t1*t2=3
=>t1;t2 là nghiệm của pt
T^2-4T+3=0
b) đenta=(2m+1)^2-4(m^2+m-1)=5>0
=>pt luôn luôn có nghiệm với mọi m
c) A=(2x1-x2)(2x2-x1)=5x1x2-2x1^2-2x2^2=5x1x2-2(x1^2+x2^2)=5x1x2-2(x1+x2)^2+4x1x2=9x1x2-2(x1+x2)^2
=9(m^2+m-1)-2(2m+1)^2=9m^2+9m-9-4m-2=9m^2+5m-11>=-421/36 khi x=-5/18
Chọn A
Ta có z = 1 - 2i là nghiệm của phương trình đã cho nên:
( 1 - 2 i ) 2 + a ( 1 - 2 i ) + b = 0 <=> (a + b - 3) - (2a + 4)i = 0
Vậy: a + b = -2 + 5 = 3