
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

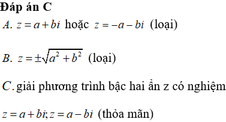

Câu 1:
Vì \(ab=\frac{a}{b}\Rightarrow a=\frac{a}{b^2}\Rightarrow\frac{a}{a}=b^2\Rightarrow b^2=1\Rightarrow b\epsilon\left\{-1;1\right\}\)
Với b=-1
=> a+(-1)=a/-1
=> a-1=-a
=> a-(-a)=1
=> 2a=1
=> \(a=\frac{1}{2}\)
Với b=1
=> a+1=a/1=a (vô lý)
Vậy a=1/2; b=-1

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

ta có \(A=\frac{yz\sqrt{x-1}+xz\sqrt{y-2}+xy\sqrt{z-3}}{xyz}=\frac{\sqrt{x-1}}{x}+\frac{\sqrt{y-2}}{y}+\frac{\sqrt{z-3}}{z}\)
\(=\sqrt{\frac{1}{x}-\frac{1}{x^2}}+\sqrt{\frac{1}{y}-\frac{2}{y^2}}+\sqrt{\frac{1}{z}-\frac{3}{x^2}}=\sqrt{\frac{1}{4}-\left(\frac{1}{x^2}-2.\frac{1}{2}x+\frac{1}{4}\right)}+\sqrt{\frac{1}{8}-\left(\left(\sqrt{2}y\right)^2-2.\frac{\sqrt{2}}{2\sqrt{2}}x+\frac{1}{8}\right)}+\sqrt{\frac{1}{2}-\left(\left(\sqrt{3}z\right)^2-\frac{1}{z}+\frac{1}{12}\right)}\)
\(=\sqrt{\frac{1}{4}-\left(\frac{1}{x}-\frac{1}{2}\right)^2}+\sqrt{\frac{1}{8}-\left(\frac{\sqrt{2}}{y}-\frac{1}{2\sqrt{2}}\right)^2}+\sqrt{\frac{1}{12}-\left(\frac{\sqrt{3}}{z}-\frac{1}{2\sqrt{3}}\right)^2}\)
ta có \(\sqrt{\frac{1}{4}-\left(\frac{1}{x}-\frac{1}{2}\right)^2}\le\frac{1}{2}\) ; \(\sqrt{\frac{1}{8}-\left(\frac{\sqrt{2}}{y}-\frac{1}{2\sqrt{2}}\right)^2}\le\frac{1}{2\sqrt{2}}\); \(\sqrt{\frac{1}{12}-\left(\frac{\sqrt{3}}{z}-\frac{1}{2\sqrt{3}}\right)^2}\le\frac{1}{2\sqrt{3}}\)
vậy giá trị lớn nhất của A =\(\frac{1}{2}+\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{3}}\) khi x=; y=4;z=6

Đáp án D
z + 2 + i − z ( 1 + i ) = 0 ⇔ ( a + b i ) + 2 + i − a 2 + b 2 ( 1 + i ) = 0 ⇔ a + 2 − a 2 + b 2 + ( b + 1 − a 2 + b 2 ) i = 0 ⇒ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇒ a − b + 1 = 0 ⇒ a = b − 1 ⇒ b + 1 − ( b − 1 ) 2 + b 2 = 0 ⇒ 2 b 2 − 2 b + 1 = b + 1 ⇒ b ≥ − 1 b 2 − 4 b = 0 ⇒ b = 0 b = 4 ⇒ a = − 1 ( L ) a = 3 ⇒ P = 4 + 3 = 7