cho 3 tập hợp các số nguyên dương bất kỳ A,B,C Chứng minh rằng: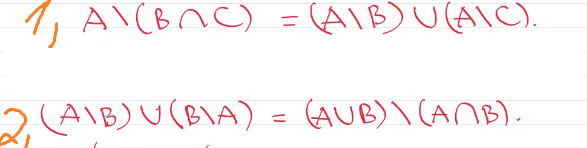
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HA
0
Những câu hỏi liên quan
16 tháng 2 2016
M=a/a+b+b/b+c+c/c+a vs a,b,c lớn hơn 0
M=1+b+1+c+1+a=3+a,b,c
M là số nguyên
HP
16 tháng 2 2016
Ta có a/b+c+b/a+c+c/a+b > a/a+b+c+b/b+c+a+c/b+c+a=a+b+c/a+b+c=1
=>M>1
Lại có M=(1-b/a+b)+(1- c/b+c)+(1-c/a+c)<3-(b/a+b+c+c/b+c+a+a/c+a+b)=3-1=2
=>M < 2
do đo 1<M<2=>đpcm
28 tháng 3 2016
do tong 5 so nguyen bat ki la 1 SND nen co it nhat 1 SND.Trong 31 so ta lay ra 1 nhom gom 5 SN khi do ton tai it nhat 1 SN,ta tach so nguyen do ra.Nhu vay ton tai 30 SN.ta nhom 5 SN vao 1 nhom nen co so nhom la 30 : 5 =6(nhom)do tong moi nhom la 1 so nguyen duong nen tong 6 nhom la 1 SND hay tong 30 so la SND.ta cong SND tach ra luc dau vao co 31 so la SND
29 tháng 6 2015
Trong 31 số đã cho có ít nhất 1 số là số dương (vì nếu 31 số đã cho đều âm thì tổng của 5 số bất kỳ không thể là 1 số dương)
Tách riêng số dương đó ra còn 30 số, nhóm 5 số vào 1 nhóm thì được 6 nhóm. Trong đó nhóm nào cũng là 1 số dương.
=> Tổng của 30 số là 1 số dương cộng thêm 1 số dương đã tách.
Vậy tổng của 31 số đó là 1 số dương
29 tháng 6 2015
Cách 1 :Trong 31 số đã cho có ít nhất 1 số là số dương (vì nếu 31 số đã cho đều âm thì tổng của 5 số bất kỳ không thể là 1 số dương)
Tách riêng số dương đó ra còn 30 số, nhóm 5 số vào 1 nhóm thì được 6 nhóm. Trong đó nhóm nào cũng là 1 số dương.
=> Tổng của 30 số là 1 số dương cộng thêm 1 số dương đã tách.
Vậy tổng của 31 số đó là 1 số dương
Cách 2 :Trong các số đã cho ít nhất có 1 số dương vì nếu trái lại tất cả đều là số âm thì tổng của 5
số bất kỳ trong chúng sẽ là số âm trái với giả thiết.
Tách riêng số dương đó còn 30 số chi làm 6 nhóm. Theo đề bài tổng các số của mỗi nhóm đều là số
dương nên tổng của 6 nhóm đều là số dương và do đó tổng của 31 số đã cho đều là số dương.
6 tháng 1 2016
Giả sử trong 31 số nguyên dương đã cho có a số nguyên âm.
Ta thấy a ≤ 4 (vì nếu a ≥ 5 thì tổng của 5 số nguyên âm sẽ là một số nguyên âm. Điều này trái với đề bài là tổng của 5 số bất kỳ là một số dương). Lấy ra a số nguyên âm này và (5-a) số nguyên dương thì sẽ tạo ra nhóm gồm 5 số và tổng của 5 số này là số dương (gọi là m)
Còn 31-5=26 số nguyên dương và tổng của của chúng là số dương (gọi là n)
Vì m>0 và n>0 => m+n>0 => tổng của 31 số đã cho là một số dương.
3 tháng 7 2016
Trong 31 số đã cho có ít nhất 1 số là số dương (vì nếu 31 số đã cho đều âm thì tổng của 5 số bất kỳ không thể là 1 số dương)
Tách riêng số dương đó ra còn 30 số, nhóm 5 số vào 1 nhóm thì được 6 nhóm. Trong đó nhóm nào cũng là 1 số dương.
=> Tổng của 30 số là 1 số dương cộng thêm 1 số dương đã tách.
Vậy tổng của 31 số đó là 1 số dương