Biết I = ∫ 0 4 x ln 2 x + 1 d x = a b ln 3 - c , trong đó a, b, c là các số nguyên dương và a b là phân số tối giản. Tính S = a + b + c.
A. S = 60
B. S = 70
C. S = 72
D. S = 68
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 5 2018
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:
NH
6 tháng 11 2023
a) \(\int\dfrac{2dx}{x^2-5x}=\int\left(\dfrac{-2}{5x}+\dfrac{2}{5\left(x-5\right)}\right)dx=-\dfrac{2}{5}ln\left|x\right|+\dfrac{2}{5}ln\left|x-5\right|+C\)
\(\Rightarrow A=-\dfrac{2}{5};B=\dfrac{2}{5}\Rightarrow2A-3B=-2\)
b) \(\int\dfrac{x^3-1}{x+1}dx=\int\dfrac{x^3+1-2}{x+1}dx=\int\left(x^2-x+1-\dfrac{2}{x+1}\right)dx=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2+x-2ln\left|x+1\right|+C\)
\(\Rightarrow A=\dfrac{1}{3};B=\dfrac{1}{2};E=-2\Rightarrow A-B+E=-\dfrac{13}{6}\)
CM
11 tháng 3 2018
a) Bất phương trình đã cho tương đương với hệ sau:
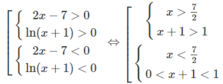
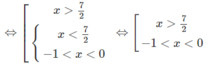
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
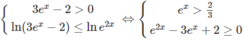
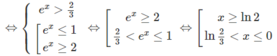
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
a) Điều kiện: \(\left\{{}\begin{matrix}4x+2>0\\x-1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>1\)
Khi đó biến đổi pương trình như sau:
\(\ln\dfrac{4x+2}{x-1}=\ln x\)
\(\Leftrightarrow\dfrac{4x+2}{x-1}=x\)
\(\Leftrightarrow4x+2=x\left(x-1\right)\)
\(\Leftrightarrow x^2-5x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{5+\sqrt{33}}{2}\\x_2=\dfrac{5-\sqrt{33}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình là: \(x=\dfrac{5+\sqrt{33}}{2}\)
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
b) Điều kiện: \(\left\{{}\begin{matrix}3x+1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>0\)
Biến đổi phương trình như sau:
\(\log_2\left(3x+1\right)\log_3x-2\log_2\left(3x+1\right)=0\)
\(\Leftrightarrow\log_2\left(3x+1\right)\left(\log_3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\log_2\left(3x+1\right)=0\\\log_3x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=2^0\\x=3^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=9\end{matrix}\right.\)
Vậy nghiệm là x = 9.
Đáp án B.
Đặt ln 2 x + 1 = u x d x = d v ⇒ 2 2 x + 1 d x = d u v = x 2 2 ⇒ 1 x + 1 2 d x = d u v = x 2 - 1 / 4 2
⇒ I = x 2 2 ln 2 x + 1 0 4 - 1 2 ∫ 0 4 x - 1 2 d x = 63 ln 3 4 - 3 ⇒ a + b + b = 70 .