Cho tam giác ABC, trung tuyến AM và trọng tâm G. Khẳng định nào sau đây là đúng?
A. A M → = 2 A B → + A C →
B. M G → = 3 M A → + M B → + M C →
C. A M → = - 3 G M →
D. A G → = 1 3 A B → + A C →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Do G là trọng tâm tam giác và trung tuyến AM nên AM = 3GM.
Suy ra: A M → = - 3 M G →
Đáp án D

Cho tam giác ABC có AM và BN là hai đường trung tuyến cắt nhau tại G. Khẳng định nào sau đây đúng? (có thể chọn nhiều đáp án) *
Điểm G cách đều ba đỉnh của tam giác
Điểm G gọi là trọng tâm của tam giác
GA = 2.GM
Điểm G cách đỉnh B một khoảng bằng 2/3 độ dài đường trung tuyến BN
GA = GB
GN = 3.BN

Nếu G là trong tâm tam giác ABC thì
G A → + G B → + G C → = 0 → ⇔ A G → + B G → + C G → = 0 → ⇔ A G → + B G → + C G → = 0 → = 0
Đáp án C

+ G là trọng tâm của tam giác DEF với đường trung tuyến DH.
Theo tính chất đường trung tuyến
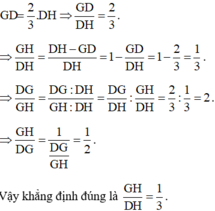

Vì `G` là trọng tâm của tam giác
`@` Theo tính chất của trọng tâm (cách đỉnh `2/3,` cách đáy `1/3`)
`-> GA = 2GM, GA= 2/3 AM`
Xét các đáp án trên `-> D.`