Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó A G → bằng
A. 1 2 G M →
B. - 1 3 A M →
C. 2 3 A M →
D. - 2 3 A M →
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2023
cho tam giác ABC coa đường trung tuyến AM và trọng tâm G . khi đó tỉ soo GM/AG bằng :
A, 1/3
B,2/3
C,1/2
D,2
12 tháng 3 2023
Theo định lý trọng tâm của đường trung tuyến:
`-` Trọng tâm của tam giác cách đỉnh `2/3,` cách đáy `1/3`
Vì `G` là trọng tâm của tam giác `ABC -> AG=2/3 AM, GM=1/3 AM`
`->` Tỉ số của \(\dfrac{GM}{AG}=\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{2}{3}\right)}=\dfrac{1}{2}\)
`-> C`
S
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
DA
18 tháng 5 2021
Xét tam giác ABC, ta có:
Đtt AM (gt)
G là trọng tâm (gt)
=> G thuộc AM ( t/c)
=> 3 điểm A,G,M thẳng hàng (đpcm)
.Mặt khác 
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
19 tháng 9 2018
\(AG=\frac{2}{3}AM=IG\)
\(MG=\frac{1}{3}AM\) mà \(IM=IG-MG=\frac{2}{3}AM-\frac{1}{3}AM=\frac{1}{3}AM\)
\(\Rightarrow MG=IM=\frac{1}{3}AM\) => I đối xứng với G qua M
CM
28 tháng 4 2019
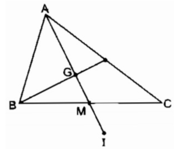
I đối xứng với A qua tâm G
ta có: GA = GI, GM ∈ GA ( tính chất đường trung tuyến của tam giác)
Suy ra: GM ∈ GI
Mà: GM + MI = GI và GM = AG/2 (tính chất đường trung tuyến) =>GM = GI/2
Suy ra: GM = MI nên điểm M là trung điểm của GI
Vậy I đối xứng với G qua M.
Vì G là trọng tâm tam giác ABC nên: A G → = 2 3 A M →
Đáp án C