Hãy so sánh
a) 2 3 5 và 2 7 9
b) − 1 2 3 và − 7 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
13 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
7 tháng 9 2021
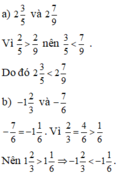
\(1,\\ a,2< 3\Rightarrow2^{30}< 3^{30}\Rightarrow-2^{30}>-3^{30}\\ b,6^{10}=6^{2\cdot5}=\left(6^2\right)^5=36^5>35^5\left(36>35\right)\)
\(2,\\ a,\dfrac{\left(-3\right)^{10}\cdot15^5}{25^3\cdot\left(-9\right)^7}=\dfrac{3^{10}\cdot5^5\cdot3^5}{5^6\cdot3^{14}}=\dfrac{3}{5}\\ b,\left(8x-1\right)^{2x+1}=5^{2x+1}\\ \Leftrightarrow8x-1=5\\ \Leftrightarrow x=\dfrac{3}{4}\)
7 tháng 9 2021
Bài 2:
a: Ta có: \(\dfrac{\left(-3\right)^{10}\cdot15^5}{25^3\cdot\left(-9\right)^7}\)
\(=\dfrac{-3^{10}\cdot3^5\cdot5^5}{5^6\cdot3^{14}}\)
\(=-\dfrac{3}{5}\)
b: Ta có: \(\left(8x-1\right)^{2x+1}=5^{2x+1}\)
\(\Leftrightarrow8x-1=5\)
\(\Leftrightarrow8x=6\)
hay \(x=\dfrac{3}{4}\)
28 tháng 9 2021
a) \(3\sqrt{3}=\sqrt{27}>\sqrt{12}\)
b) \(3\sqrt{5}=\sqrt{45}>\sqrt{27}\)
c) \(\dfrac{1}{3}\sqrt{51}=\sqrt{\dfrac{51}{9}}< \sqrt{\dfrac{54}{9}}=6=\sqrt{\dfrac{150}{25}}=\dfrac{1}{5}\sqrt{150}\)
d) \(\dfrac{1}{2}\sqrt{6}=\sqrt{\dfrac{6}{4}}=\sqrt{\dfrac{3}{2}}< \sqrt{\dfrac{36}{2}}=6\sqrt{\dfrac{1}{2}}\)
TN
1
8 tháng 11 2021
a) \(2=\sqrt{4}>\sqrt{3}\)
b) \(6=\sqrt{36}< \sqrt{41}\)
c) \(7=\sqrt{49}>\sqrt{47}\)
LB
1
6 tháng 11 2021
b: \(\dfrac{3}{\sqrt{7}-2}-\dfrac{4}{\sqrt{7}+\sqrt{3}}\)
\(=\sqrt{7}+2-\sqrt{7}+\sqrt{3}=2+\sqrt{3}\)
GH
22 tháng 6 2023
a)
Có:
\(2\sqrt{29}=\sqrt{4.29}=\sqrt{116}\\ 3\sqrt{13}=\sqrt{9.13}=\sqrt{117}\)
Vì \(\sqrt{117}>\sqrt{116}\) nên \(3\sqrt{13}>2\sqrt{29}\)
b)
Có:
\(\dfrac{5}{4}\sqrt{2}=\sqrt{\dfrac{25}{16}.2}=\sqrt{\dfrac{25}{8}}\)
\(\dfrac{3}{2}\sqrt{\dfrac{3}{2}}=\sqrt{\dfrac{9}{4}.\dfrac{3}{2}}=\sqrt{\dfrac{27}{8}}\)
Do \(\sqrt{\dfrac{27}{8}}>\sqrt{\dfrac{25}{8}}\) nên \(\dfrac{3}{2}\sqrt{\dfrac{3}{2}}>\dfrac{5}{4}\sqrt{2}\)
c)
Có:
\(5\sqrt{2}=\sqrt{25.2}=\sqrt{50}\)
\(4\sqrt{3}=\sqrt{16.3}=\sqrt{48}\)
Vì \(\sqrt{50}>\sqrt{48}\) nên \(5\sqrt{2}>4\sqrt{3}\)
d)
Có:
\(\dfrac{5}{2}\sqrt{\dfrac{1}{6}}=\sqrt{\dfrac{25}{4}.\dfrac{1}{6}}=\sqrt{\dfrac{25}{24}}\)
\(6\sqrt{\dfrac{1}{37}}=\sqrt{36.\dfrac{1}{37}}=\sqrt{\dfrac{36}{37}}\)
lại có: \(\dfrac{25}{24}>\dfrac{36}{37}\)
\(\Rightarrow\dfrac{5}{2}\sqrt{\dfrac{1}{6}}>6\sqrt{\dfrac{1}{37}}\)
TL
2
T
26 tháng 8 2023
\(a,2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
Vì \(8^{100}< 9^{100}\) nên \(2^{300}< 3^{200}\)
\(b,8^5=32768\)
\(6^6=46656\)
Vì \(32768< 46656\) nên \(8^5< 6^6\)
\(c,3^{450}=\left(3^3\right)^{150}=27^{150}\)
\(5^{300}=\left(5^2\right)^{150}=25^{150}\)
Vì \(27^{150}>25^{150}\) nên \(3^{450}>5^{300}\)
#Ayumu
29 tháng 12 2017
a, Chia hết cho 3 thì nhóm 2 số thành 1 cặp ; chia hết cho 7 thì nhóm 3 số thành 1 cặp
b, Đề phải là A = 2009.2011
Có :A = 2009.(2010+1) = 2009.2010+2009
= 2009.2010+2010-1 = 2010.(2009+1)-1 = 2010^2-1
Vì 2010^2-1 < 2010^2 = B => A < B
c, A = (3^3)^150 = 27^150
B = (5^2)^150 = 25^150
Vì 27^150 > 25^150 => A > B
k mk nha
11 tháng 2 2017
A=1+2+2^2+2^3+....+2^9
2A=2+2^2+2^3+....+2^10
2A-A=2^10-1
A=2^10-1/2
B=5.2^8=(2^2+1).2^8=2^10+2^8
=>B>A
11 tháng 2 2017
2A = 2(1 + 2 + 22 + .... + 29 )
= 2 + 22 + 23 + ..... + 210
2A - A = (2 + 22 + 23 + ..... + 210) - (1 + 2 + 22 + .... + 29 )
A = 210 - 1
B = 5.28 = (22 + 1).28 = 210 + 28
210 - 1 < 210 + 28
=> A < B
7 tháng 7 2021
a) \(\dfrac{-1}{20}=\dfrac{-7}{140}\)
\(\dfrac{5}{7}=\dfrac{100}{140}\)
mà -7<100
nên \(-\dfrac{1}{20}< \dfrac{5}{7}\)
b) \(\dfrac{216}{217}< 1\)
\(1< \dfrac{1164}{1163}\)
nên \(\dfrac{216}{217}< \dfrac{1164}{1163}\)
c) \(\dfrac{-12}{17}=\dfrac{-180}{255}\)
\(\dfrac{-14}{15}=\dfrac{-238}{255}\)
mà -180>-238
nên \(-\dfrac{12}{17}>\dfrac{-14}{15}\)
d) \(\dfrac{27}{29}>0\)
\(0>-\dfrac{2727}{2929}\)
nên \(\dfrac{27}{29}>-\dfrac{2727}{2929}\)