Chứng minh: 1 x − 1 x 3 = 3 x ( x 3 ) . Từ đó, tính nhanh biểu thức: M= 1 x (...

PT

Pham Trong Bach

22 tháng 1 2019

Chứng minh: 1 x − 1 x + 3 = 3 x ( x + 3 ) . Từ đó, tính nhanh biểu thức: M= 1 x ( x + 3 ) + 1 ( x + 3 ) ( x + 6 ) + . .. + 1 ( x + 12 ) ( x + 15 ) , với các mẫu thỏa mãn x ≠ 0 ...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

22 tháng 1 2019

Đúng(0)

VL

Vũ Lan Anh

9 tháng 5 2021 - olm

Cho 2 biểu thức A=x+3/x+2 và B=x/x+1+2/x-1-4/x^2-1

1)Tính giá trị của biểu thức A khi x=-3

2)Chứng minh B=x+2/x+1

3)Đặt M=A.B.tÌM x để m>0

#Toán lớp 8

4

PN

Phan Nghĩa

9 tháng 5 2021

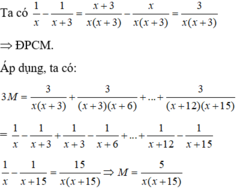
a, Do \(x=-3\)\(=>A=\frac{x+3}{x+2}=\frac{-3+3}{-3+2}=\frac{0}{-1}=0\)

Vậy A = 0 khi x = -3

b, Ta có : \(B=\frac{x}{x+1}+\frac{2}{x-1}-\frac{4}{x^2-1}=\frac{x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{2\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}-\frac{4}{x^2-1}\)

\(=\frac{x^2-x+2x-2}{x^2-1}=\frac{x\left(x-1\right)+2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\frac{\left(x+2\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)

\(=\frac{x+2}{x+1}\)(đpcm)

Đúng(0)

TM

Trần Minh Phong

9 tháng 5 2021

iophkhghoghkghjggjhghgjhjnnrjhnjvfdjgjhrthgfjhnvfgughfuihgjfdhntfjhb fdghxdfjthfgdrtfghertgfhgrthgrthgrtrgurgfhgfhgerhgdsuhtyhdfuyhrhgthfutrugerhtgtertmgiurjhtjyiujbgf89yhjrintjihjdhr hbfbv nùgvuibherufdhtguihruvhaweufhvnfgffyhrghsr78ryughg9u8ghtityjyhyijtyjuy8hituhzihuyuyru9jr0ujtyututr09yuitutr9uirt9ui56i789i69utihirrgiu6ygjityojhojkyjyykikgjkthogfjkjhfggfjkhjkhkjkjkjkjgfohfkojhiyy0jhiuihmokhmhjkhkjykkhjkhjykjkgjkyjyotuhjnhknkhijiyjiyitihfgujdhufturgjjhi htfhrhfgrhuygrutrtuyhrthuyhrhtuhutryjuy.ôl

Đúng(0)

NJ

Nhok Jans

5 tháng 12 2016 - olm

Tính nhanh: 37x43

Chứng minh các biểu thức sau ko phụ thuộc vào biến: C= (x-1)^3 - (x+1)^3 + 6(x+1)(x-1)

giải giúp em với, em đang cần gấp ạ ^^ <3

#Toán lớp 8

0

ES

erza sarlet

6 tháng 9 2017

1/Rút gọn biểu thức: (x+5)^3-x^3-125

2/ Tìm x biết(x-2)^3+6(x-1)^2-x^3+12=0

3/ Chứng minh rằng biểu thức sau ko phụ thuộc vào x

A=(x-1)^3-x^3-3x^2-3x-1

#Toán lớp 8

1

ES

erza sarlet

6 tháng 9 2017

câu 2( x-1) đổi thành (x+1).

Đúng(0)

ES

erza sarlet

7 tháng 9 2017

1/Rút gọn biểu thức: (x+5)^3-x^3-125

2/ Tìm x biết(x-2)^3+6(x+1)^2-x^3+12=0

3/ Chứng minh rằng biểu thức sau ko phụ thuộc vào x

A=(x-1)^3-x^3-3x^2-3x-1

#Toán lớp 8

1

TN

T.Thùy Ninh

7 tháng 9 2017

\(1,\left(x+5\right)^3-x^3-125\)

\(=x^3+15x^2+75x+125-x^3-125\)

\(=15x\left(x+5\right)\)

\(2,\left(x-2\right)^3+6\left(x+1\right)^2-x^3+12=0\)

\(\Leftrightarrow x^3-6x^2+12x-8+6x^2+12x+6-x^3+12=0\)\(\Leftrightarrow24x+10=0\)

\(\Leftrightarrow24x=-10\)

\(\Leftrightarrow x=-\dfrac{5}{12}\)

\(3,A=\left(x-1\right)^3-x^3-3x^2-3x-1\)

\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1\)

\(=-6x^2-2\)

#đề.bài.sai.không.bạn

Đúng(0)

ES

erza sarlet

7 tháng 9 2017

đề sai rồi. Bài 1 kết quả=15^2+75x ms đúng

Đúng(0)

T

Toru

19 tháng 11 2023

Cho biểu thức:

\(A=\dfrac{x^2+1}{x}+\dfrac{x^3-1}{x^2-x}+\dfrac{x^4-x^3+x-1}{x-x^3}\left(x>0;x\ne1\right)\)

a) Rút gọn A

b) Tìm A biết x thoả mãn: \(x^2+x=12\)

c) Chứng minh rằng: \(A>4\). Từ đó tìm x để \(B=\dfrac{6}{A}\) nhận giá trị nguyên

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 11 2023

a: \(A=\dfrac{x^2+1}{x}+\dfrac{x^3-1}{x^2-x}+\dfrac{x^4-x^3+x-1}{x-x^3}\)

\(=\dfrac{x^2+1}{x}+\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}-\dfrac{x^3\left(x-1\right)+\left(x-1\right)}{x\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{x^2+1}{x}+\dfrac{x^2+x+1}{x}-\dfrac{\left(x-1\right)\left(x^3+1\right)}{x\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{x^2+1+x^2+x+1}{x}-\dfrac{x^2-x+1}{x}\)

\(=\dfrac{2x^2+x+2-x^2+x-1}{x}=\dfrac{x^2+2x+1}{x}=\dfrac{\left(x+1\right)^2}{x}\)

b: \(x^2+x=12\)

=>\(x^2+x-12=0\)

=>(x+4)(x-3)=0

=>\(\left[{}\begin{matrix}x+4=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-4\left(loại\right)\end{matrix}\right.\)

Thay x=3 vào A, ta được:

\(A=\dfrac{\left(3+1\right)^2}{3}=\dfrac{16}{3}\)

Khi x=-4 thì \(A=\dfrac{\left(-4+1\right)^2}{-4}=\dfrac{9}{-4}=-\dfrac{9}{4}\)

c: \(A-4=\dfrac{\left(x+1\right)^2}{x}-4\)

\(=\dfrac{\left(x+1\right)^2-4x}{x}\)

\(=\dfrac{x^2+2x+1-4x}{x}=\dfrac{x^2-2x+1}{x}=\dfrac{\left(x-1\right)^2}{x}\)>0 với mọi x>0

=>A>4

Đúng(3)

T

Toru

19 tháng 11 2023

Cảm ơn anh mà anh giải nốt phần cuối nữa được không ạ?

Đúng(0)

NT

Nguyễn Thị Thùy

27 tháng 8 2016 - olm

Chứng minh giá trị biểu thức sau:

M = (x – 1)(x – 2)(x – 3) + (x – 1)(x – 2) + (x – 1)

#Toán lớp 8

0

VD

Võ Dương Vĩnh Thắng

5 tháng 11 2016

1) Xác định số a,b để đa thức x^4-3x^3+3x^2 +ax+b chia hết cho đa thức x^2-3x+42)Cho x+y=1.Tính giá trị của biểu thức: A=x^3+y^3+3xy3)Tình già trị của biểu thức M=x^6 -2x^4+x^3+x^2-x biết x^3-x=84)Chứng minh rằng lập phương của một số nguyên cộng với 17 lần số đó một số chia hết cho 65) Chứng minh các biểu thức sau không phụ thuộc vào biến số x:-x(x+2y)+(x+y)^2+(x-5)^2-(x-2)(x-8)+(3x-2)^2+3x(4-3x)6) Cho...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

6 tháng 2 2022

Bài 2:

\(A=\left(x+y\right)^3-3xy\left(x+y\right)+3xy=1^3-3xy+3xy=1\)

Bài 3:

\(M=x^6-x^4-x^4+x^2+x^3-x\)

\(=x^3\left(x^3-x\right)-x\left(x^3-x\right)+\left(x^3-x\right)\)

\(=8x^3-8x+8\)

\(=8\cdot8+8=72\)

Đúng(0)

XP

Xuyen Phan

12 tháng 7 2021

Tính nhanh

b) 98^2

chứng minh các biểu thức không phụ thuộc giá trị của biến

A) (x+3)^2 - (x-3)^2-12

B) (x-2)^2 - (x -3) (x-1)

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 7 2021

b)\(98^2=\left(100-2\right)^2=10000-400+4=9604\)

Bài 2:

a) Ta có: \(\left(x+3\right)^2-\left(x-3\right)^2-12x\)

\(=x^2+6x+9-x^2+6x-9-12x\)

=0

b) Ta có: \(\left(x-2\right)^2-\left(x-3\right)\left(x-1\right)\)

\(=x^2-4x+4-x^2+4x-3\)

=-1

Đúng(2)

BA

Bạch An Nhiên

8 tháng 10 2017

1) Chứng minh biểu thức sau không phụ thuộc vào biến
a) A = ( x-1)^3 - (x+4) ( x^2 - 4x + 16 ) + 3x(x-1)
b) B = ( x+y - 1)^3 - (x+y+1)^3 + 6(x+y)
2) Tìm GTNN của biểu thức
A = x^2 + 6x + 11
Tìm giá trị lớn nhất của biểu thức
B = 4-x^2 - x

#Toán lớp 8

2

PT

Phương Trâm

8 tháng 10 2017

1.

a) \(A=\left(x-1\right)^3-\left(x+4\right)\left(x^2-4x+16\right)+3x\left(x-1\right)\)

\(A=\left(x^3-3x^2+3x-1\right)-\left(x^3+64\right)+\left(3x^2-3x\right)\)

\(A=x^3-3x^2+3x-1-x^3-64+3x^2-3x\)

\(A=\left(x^3-x^3\right)+\left(-3x^2+3x\right)+\left(3x-3x\right)+\left(-1-64\right)\)

\(A=-65\)

Vậy giá trị của biểu thức trên không phụ thuộc vào biến.

b) \(B=\left(x+y-1\right)^3-\left(x+y+1\right)^3+6\left(x+y\right)^2\)

\(B=\left[\left(x+y-1\right)-\left(x+y+1\right)\right].\left[\left(x+y-1\right)^2+\left(x+y-1\right).\left(x+y+1\right)+\left(x+y+1\right)^2\right]+6\left(x+y\right)^2\)

\(B=\left(x+y-1-x-y-1\right).\left[\left(x+y\right)^2-2\left(x+y\right).1+1+\left(x+y\right)^2-1+\left(x+y\right)^2+2\left(x+y\right).1+1\right]+6\left(x+y\right)^2\)

\(B=-2.\left(x^2+2xy+y^2-2x-2y+1+x^2+2xy+y^2-1+x^2+2xy+y^2+2x+2y+1\right)+6\left(x+y\right)^2\)

\(B=-2.\left(3x^2+6xy+3y^2+1\right)+6\left(x+y\right)^2\)

\(B=-2.\left(3x^2+6xy+3y^2\right)-2+6\left(x+y\right)^2\)

\(B=-6\left(x+y\right)^2+6\left(x+y\right)^2-2\)

\(B=-6\left[\left(x+y\right)^2-\left(x+y\right)^2\right]-2\)

\(B=-2\)

Vậy giá trị của biểu thức trên không phụ thuộc vào biến.

2. \(A=x^2+6x+11\)

\(A=x^2+2x.3+3^2+2\)

\(A=\left(x+3\right)^2+2\)

Ta có: \(\left(x+3\right)^2\ge0\)

\(\Rightarrow\left(x+3\right)^2+2\ge2\)

\(\Rightarrow Min_A=2\Leftrightarrow x=-3\)

\(B=4-x^2-x\)

\(B=-x^2-x+4\)

\(B=-x^2-x-\dfrac{1}{4}+\dfrac{17}{4}\)

\(B=-\left(x^2+2x.\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{17}{4}\)

\(B=-\left(x+\dfrac{1}{2}\right)^2+\dfrac{17}{4}\)

Ta có: \(-\left(x+\dfrac{1}{2}\right)^2\le0\)

\(\Rightarrow-\left(x+\dfrac{1}{2}\right)^2+\dfrac{17}{4}\le\dfrac{17}{4}\)

\(\Rightarrow Max_B=\dfrac{17}{4}\Leftrightarrow x=-\dfrac{1}{2}\)

Đúng(0)

NH

Nguyễn Huy Đức

8 tháng 10 2017

i

111111	1111
111111	1111
111111	1111

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP