Gọi O là tâm hình bình hành ABCD; hai điểm E; F lần lượt là trung điểm AB; BC. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
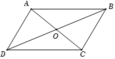
+ Đáp án A. Ta có ![]() . Vậy A đúng.
. Vậy A đúng.
+ Đáp án B. Ta có 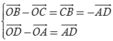 . Vậy B sai.
. Vậy B sai.
+ Đáp án C. Ta có ![]() .Vậy C đúng.
.Vậy C đúng.
+ Đáp án D. Ta có 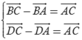 . Vậy D đúng.
. Vậy D đúng.

Lời giải:
Vì $ABCD$ là hình bình hành nên tâm $O$ là trung điểm $AC$
$\Rightarrow OK$ là đường trung bình của $SAC$ ứng với cạnh $SA$
$\Rightarrow OK\parallel SA$
Mà $SA\subset (SAB)$ nên $OK\parallel (SAB)$
Ta có OF; OE lần lượt là đường trung bình của tam giác BCD và ABC.
Suy ra BEOFlà hình bình hành