Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

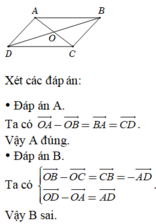
Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)
Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)
Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)
a) Bằng vectơ AB :
\(\overrightarrow{DC}\)
Bằng vectơ OB :
\(\overrightarrow{DO}\)
b)Có độ dài bằng OB :
\(\overrightarrow{OD},
\overrightarrow{DO},
\overrightarrow{BO}\)

A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \nRightarrow \frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \(\sin B = \frac{{\sqrt 2 }}{2}\))
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\({b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \(\widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \({b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
=> D đúng.
Chọn D

1. Kẻ đường kính chứa 1 trong 3 điểm A,B,C bất kỳ của (O)
Tam giác ABC chứa tâm O <=>
(*) Có nhiều nhất 2 điểm nằm
trên nửa đường tròn (O) có đường kính như trên , không nhận
cạnh nào là đường kính
(*) ABC là tam giác vuông
Nhận thấy khi tam giác ABC nội tiếp (O) thì A,B,C có 3 trường hợp:
TH1 : 3 điểm cùng nằm trên nửa (O ; DE/2) , không có cạnh nào là đường kính
TH2 : 2 điểm nằm trên nửa (O ; DE/2) ; 1 điểm trên nửa (O) còn lại
TH3 : Tam giác vuông
Biến cố A : " Tam giác ABC chứa tâm O"
=> P(A) = \(\dfrac{2}{3}\)

Tham khảo ạ !!!!
vì các góc ACD và ABD đều nhìn đoạn AD dưới 1 góc vuông
suy ra góc ACD = ABD = 90
vì H là trực tâm tam giác
suy ra BH vuông góc với AC
và CH vuông góc với AB
vì BH vuông góc với AC
mà CD vuông góc với AC
suy ra BH//CD
tương tự, ta được BD//HC
suy ra tứ giác BHCD là hình bình hành
suy ra BH = CD
mà BH//CD(cmt)
suy ra vecto BH = DC

1: A(2;0); B(-3;4); C(1;-5)
Tọa độ vecto AB là:
\(\left\{{}\begin{matrix}x=-3-2=-5\\y=4-0=4\end{matrix}\right.\)
=>\(\overrightarrow{AB}=\left(-5;4\right)\)
Tọa độ vecto AC là:
\(\left\{{}\begin{matrix}x=1-2=-1\\y=-5-0=-5\end{matrix}\right.\)
Vậy: \(\overrightarrow{AC}=\left(-1;-5\right)\)
\(\overrightarrow{AB}=\left(-5;4\right)\)
Vì \(\left(-1\right)\cdot\left(-5\right)=5< >-20=-5\cdot4\)
nên A,B,C không thẳng hàng
=>A,B,C là ba đỉnh của một tam giác
2: Tọa độ trọng tâm G của ΔABC là:
\(\left\{{}\begin{matrix}x=\dfrac{2-3+1}{3}=\dfrac{0}{3}=0\\y=\dfrac{0+4-5}{3}=-\dfrac{1}{3}\end{matrix}\right.\)
3:
\(\overrightarrow{AB}=\left(-5;4\right);\overrightarrow{DC}=\left(1-x;-5-y\right)\)
ABCD là hình bình hành
nên \(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}1-x=-5\\-5-y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1+5=6\\y=-5-4=-9\end{matrix}\right.\)
Vậy: D(6;-9)
4: \(\overrightarrow{MA}=\left(2-x;-y\right);\overrightarrow{MB}=\left(-3-x;4-y\right);\overrightarrow{MC}=\left(1-x;-5-y\right)\)
\(2\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\left\{{}\begin{matrix}2\left(2-x\right)+\left(-3-x\right)+3\left(1-x\right)=0\\2\left(-y\right)+\left(4-y\right)+3\left(-5-y\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4-2x-3-x+3-3x=0\\-2y+4-y-15-3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-6x+4=0\\-6y-11=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x=-4\\-6y=11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{11}{6}\end{matrix}\right.\)
vậy: \(M\left(\dfrac{2}{3};-\dfrac{11}{6}\right)\)
5:
A(2;0); B(-3;4); C(1;-5); N(x;y)
A là trọng tâm của ΔBNC
=>\(\left\{{}\begin{matrix}x_A=\dfrac{x_B+x_N+x_C}{3}\\y_A=\dfrac{y_B+y_N+y_C}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2=\dfrac{-3+1+x}{3}\\0=\dfrac{4-5+y}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2=6\\y-1=0\end{matrix}\right.\)
=>x=8 và y=1
Vậy: N(8;1)
6: A là trung điểm của BE
=>\(\left\{{}\begin{matrix}x_B+x_E=2\cdot x_A\\y_B+y_E=2\cdot y_A\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3+x_E=2\cdot2=4\\4+y_E=2\cdot0=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_E=7\\y_E=-4\end{matrix}\right.\)
Vậy: E(7;-4)

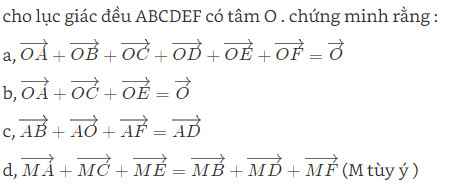
 đúng ko v ???????
đúng ko v ???????




