Mọi Người Làm Giúp Mình Với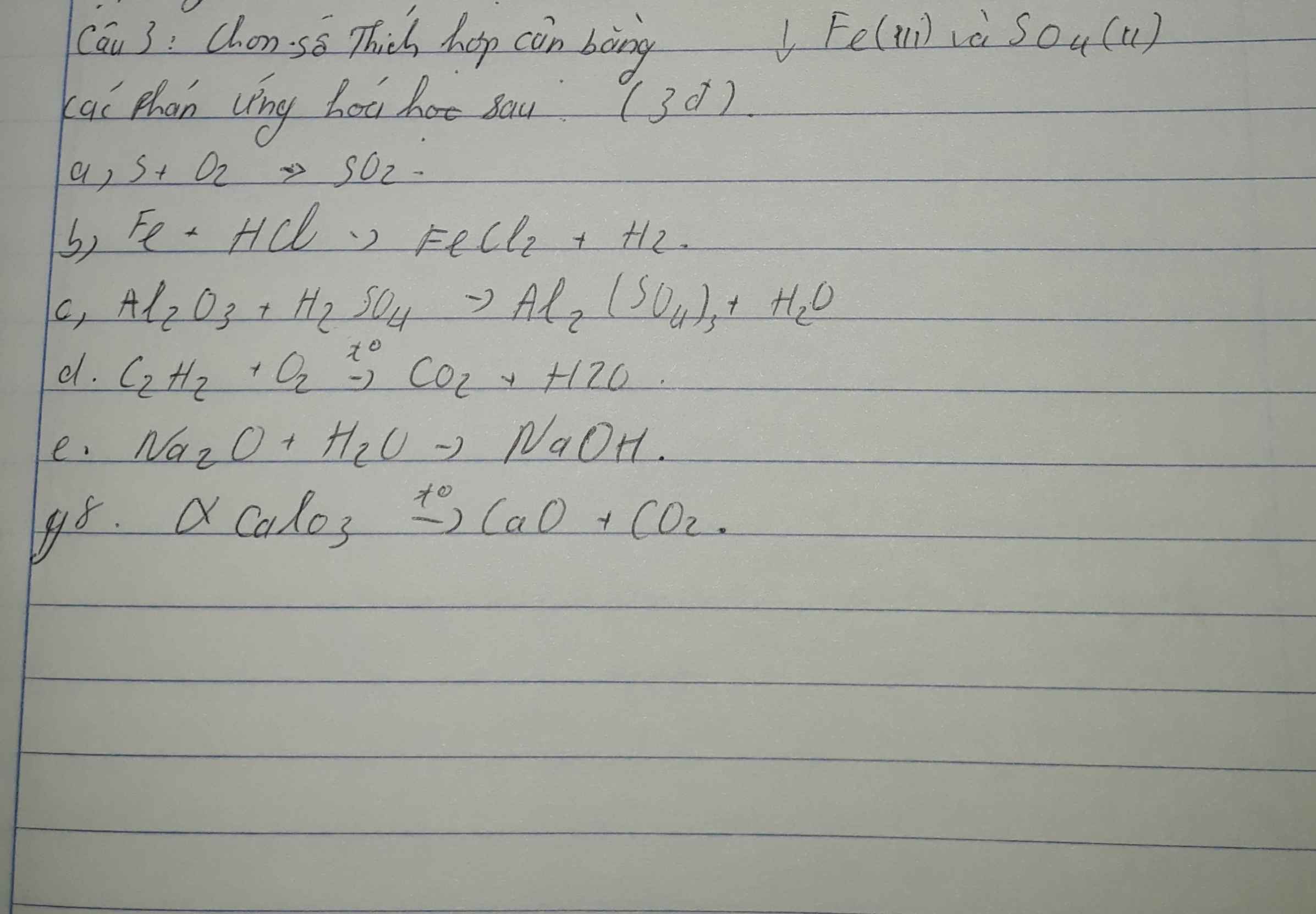
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
const fi='dulieu.dat';
fo='thaythe.out';
var f1,f2:text;
a:array[1..100]of string;
n,d,i,vt:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
n:=0;
while not eof(f1) do
begin
n:=n+1;
readln(f1,a[n]);
end;
for i:=1 to n do
begin
d:=length(a[i]);
vt:=pos('anh',a[i]);
while vt<>0 do
begin
delete(a[i],vt,3);
insert('em',a[i],vt);
vt:=pos('anh',a[i]);
end;
end;
for i:=1 to n do
writeln(f2,a[i]);
close(f1);
close(f2);
end.
Câu 2:
uses crt;
const fi='mang.inp';
fo='sapxep.out';
var f1,f2:text;
a:array[1..100]of integer;
i,n,tam,j:integer;
begin
clrscr;
assign(f1,fi); rewrite(f1);
assign(f2,fo); rewrite(f2);
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(f1,a[i]:4);
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
for i:=1 to n do
write(f2,a[i]:4);
close(f1);
close(f2);
end.

4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c


a) Ta có: \(\widehat{AOM}=90^0\)
\(\Rightarrow MO\perp AB\Rightarrow\widehat{MOB}=90^0\)
\(\Rightarrow\widehat{NOM}=\widehat{MOB}-\widehat{BON}=90^0-35^0=55^0\)
b) Ta có: \(\widehat{AOM}=90^0,\widehat{MON}=55^0,\widehat{NOB}=35^0\)
\(\Rightarrow\widehat{AOM}>\widehat{MON}>\widehat{NOB}\)
c) Cặp góc phụ nhau: \(\widehat{BON}\) và \(\widehat{MON}\)
Các cặp góc bù nhau: \(\widehat{AOM}\) và \(\widehat{MOB}\), \(\widehat{BON}\) và \(\widehat{AON}\)
Cặp góc bằng nhau: \(\widehat{AOM}\) và \(\widehat{BOM}\)
\(a,\widehat{NOM}=\widehat{BOM}-\widehat{NOB}=90^0-35^0=55^0\\ b,90^0>55^0>35^0\Rightarrow\widehat{AOM}>\widehat{MON}>\widehat{NOB}\\ c,\)
Cặp góc phụ nhau: \(\widehat{MON}.và.\widehat{NOB}\)
Cặp góc bù nhau: \(\widehat{AOM}.và.\widehat{MOB};\widehat{AON}.và.\widehat{NOB}\)
Cặp góc bằng nhau: \(\widehat{AOM}=\widehat{BOM}\left(=90^0\right)\)

Bài 2:
a: Xét ΔACM và ΔNBM có
MA=MN
\(\widehat{AMC}=\widehat{NMB}\)
MC=MB
Do đó: ΔACM=ΔNBM
b: Xét ΔAMB và ΔNMC có
MA=MN
\(\widehat{AMB}=\widehat{NMC}\)
MB=MC
Do đó: ΔAMB=ΔNMC
Suy ra: AB=CN









\(a.S+O_2\overset{t^o}{--->}SO_2\)
\(b.Fe+2HCl--->FeCl_2+H_2\)
\(c.Al_2O_3+3H_2SO_4--->Al_2\left(SO_4\right)_3+3H_2O\)
\(d.2C_2H_2+5O_2\overset{t^o}{--->}4CO_2\uparrow+2H_2O\)
\(e.Na_2O+H_2O--->2NaOH\)
\(g.CaCO_3\overset{t^o}{--->}CaO+CO_2\uparrow\)