Trục căn thức ở mẫu biểu thức 3 6 + 3 a với a ≥ 0; a ≠ 12 ta được:
A. 6 + 3 a 12 + a
B. 6 - 3 a 12 + a
C. 6 + 3 a 12 - a
D. 6 - 3 a 12 - a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

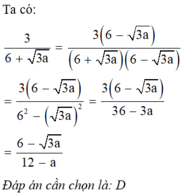


a) \(\dfrac{1+\sqrt{a}}{1-\sqrt{a}}=\dfrac{a+2\sqrt{a}+1}{1-a}\)
b) \(\dfrac{a-2\sqrt{a}}{2-\sqrt{a}}=\dfrac{-\sqrt{a}\left(2-\sqrt{a}\right)}{2-\sqrt{a}}=-\sqrt{a}\)
a) \(\dfrac{a}{3\sqrt{a}-1}=\dfrac{a\left(3\sqrt{a}+1\right)}{9a-1}\)

a: \(=5\cdot5\sqrt{3}-\dfrac{1}{3}\cdot3\sqrt{3}=24\sqrt{3}\)
b: \(=\dfrac{12\left(3+\sqrt{5}\right)}{4}=9+3\sqrt{5}\)
c: \(=3-\sqrt{5}+\sqrt{5}=3\)

\(A=\frac{2}{\sqrt[3]{2}\left(\sqrt[3]{2}^2+\sqrt[3]{2}+1\right)}=\frac{2\left(\sqrt[3]{2}-1\right)}{\sqrt[3]{2}\left(\sqrt[3]{2}^2+\sqrt[3]{2}+1\right)\left(\sqrt[3]{2}-1\right)}=\frac{2\left(\sqrt[3]{2}-1\right)}{\sqrt[3]{2}}=2-\sqrt[3]{4}\)

\(\dfrac{5}{3\sqrt{8}}=\dfrac{5}{6\sqrt{2}}=\dfrac{5.\sqrt{2}}{6.2}=\dfrac{5\sqrt{2}}{12}\)

a: \(\dfrac{\sqrt{5}}{\sqrt{7}}=\dfrac{\sqrt{5\cdot7}}{7}=\dfrac{\sqrt{35}}{7}\)
b: \(\dfrac{2}{\sqrt{a}-1}=\dfrac{2\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}=\dfrac{2\sqrt{a}+2}{a-1}\)