Tìm x, y thoả mãn: 3 x − y + 3 5 y + 9 25 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
27 tháng 12 2017
Đúng(0)
Những câu hỏi liên quan
6 tháng 11 2023
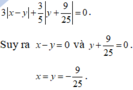
\(\left(\dfrac{3x-5}{9}\right)^{2018}>=0\forall x\)
\(\left(\dfrac{3y+0,4}{3}\right)^{2020}>=0\forall y\)
Do đó: \(\left(\dfrac{3x-5}{9}\right)^{2018}+\left(\dfrac{3y+0,4}{3}\right)^{2020}>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}\dfrac{3x-5}{9}=0\\\dfrac{3y+0,4}{3}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-5=0\\3y+0,4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=-\dfrac{0.4}{3}=-\dfrac{2}{15}\end{matrix}\right.\)
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2024
Áp dụng BĐT Cô-si:
\(x^3+x^3+8\ge3\sqrt[3]{8x^6}=6x^2\)
\(y^6+y^6+1+1+1+1\ge6\sqrt[6]{y^{12}}=6y^2\)
Cộng vế:
\(2\left(x^3+y^6\right)+12\ge6\left(x^2+y^2\right)\ge30\)
\(\Rightarrow x^3+y^6\ge9\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(2;1\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
\(\Leftrightarrow\left(x^2-6xy+9y^2\right)+\left(x^2+6x+9\right)+\left(z^2-8z+16\right)=0\)
\(\Leftrightarrow\left(x-3y\right)^2+\left(x+3\right)^2+\left(z-4\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3y=0\\x+3=0\\z-4=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-1\\z=4\end{matrix}\right.\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 10 2023
\(2^5.x+3y=32x+3y⋮7\)
Ta có
\(35x+14y⋮7\)
\(\Rightarrow\left(35x+14y\right)-\left(32x+3y\right)=3x+11y⋮7\)
LT
0
LN
Bài 1: a, Tìm GTNN của A = ∣x - 3∣ + ∣x - 4∣ + ∣x - 7∣ b, Tìm x, y thoả mãn ∣x - 2∣ + ∣ y²⁰ + 9∣ = 9
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2024
a.
\(A=\left|x-3\right|+\left|x-4\right|+\left|x-7\right|\)
\(A=\left|x-3\right|+\left|7-x\right|+\left|x-4\right|\)
Áp dụng BĐT trị tuyệt đối:
\(A\ge\left|x-3+7-x\right|+\left|x-4\right|\)
\(\Rightarrow A\ge4+\left|x-4\right|\ge4\)
\(\Rightarrow A_{min}=4\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\left(x-3\right)\left(7-x\right)\ge0\\x-4=0\end{matrix}\right.\) \(\Rightarrow x=4\)
Câu b đã giải bên dưới
NQ
0
NV
0
NT
2
17 tháng 4 2021
\(A=\frac{xyz}{x+y}\Rightarrow\frac{1}{A}=\frac{x+y}{xyz}\)
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\frac{x+y}{xyz}=\frac{x}{xyz}+\frac{y}{xyz}=\frac{1}{yz}+\frac{1}{xz}\ge\frac{\left(1+1\right)^2}{yz+xz}=\frac{4}{z\left(x+y\right)}\)(1)
Lại có \(z\left(x+y\right)\le\frac{\left(x+y+z\right)^2}{4}=\frac{9}{4}\)(theo AM-GM) => \(\frac{4}{z\left(x+y\right)}\ge\frac{16}{9}\)(2)
Từ (1) và (2) => \(\frac{x+y}{xyz}\ge\frac{4}{z\left(x+y\right)}\ge\frac{16}{9}\)=> \(\frac{x+y}{xyz}\ge\frac{16}{9}\)hay \(\frac{1}{A}\ge\frac{16}{9}\)
=> A ≤ 9/16. Đẳng thức xảy ra <=> z = 3/2 ; x = y = 3/4
Vậy MaxA = 9/16 <=> x = y = 3/4 ; z = 3/2
KC
10 tháng 5 2021
\(9=3^2=\left(x+y+z\right)^2\ge4\left(x+y\right)z\)
\(\rightarrow9.\frac{x+y}{xyz}\ge4.\frac{\left(x+y\right)^2}{xy}\ge4.\frac{4xy}{xy}=16\)
\(\rightarrow\frac{x+y}{xyz}\ge\frac{16}{9}\rightarrow\frac{xyz}{x+y}\le\frac{9}{16}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{3}{4};z=\frac{3}{2}\)