Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 11 2019
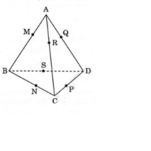
Gọi mặt cầu S(O; R) tiếp xúc với các cạnh của hình tứ diện đã cho lần lượt tại M, N, P, Q ,R và S.
* Ta chứng minh: AM = AR = AQ.
Do mặt cầu tiếp xúc với ba cạnh AB, AC và AD lần lượt tại M; R và Q nên :
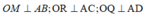
Xét ba tam giác OAM; OAR và OAQ có:
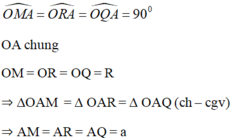
* Chứng minh tương tự ta có:
BM = BN = BS = b
CP = CN = CR = c.
DP = DQ = DS = d
Ta có:
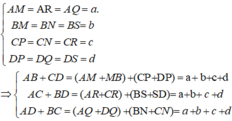
Do đó, AB + CD = AC + BD = AD + BC.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
+) Vì hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau nên tứ giác A'B'C'D'; ADD'A'; CC'D'D là hình thoi.
+) AB' // C'D và C'D \( \bot \) CD' nên AB' \( \bot \)CD'
+) AC // A'C' và A'C' \( \bot \) B'D' nên AC \( \bot \) B'D'
+) B'C // A'D và A'D \( \bot \) AD' nên B'C \( \bot \) AD'
Vậy ta đã chứng minh được rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.
CM
10 tháng 5 2017
Từ hệ thức trên ta suy ra định lí: “Nếu tứ diện ABCD có AB ⊥ CD, AC ⊥ DB, nghĩa là AB → . C D → = 0 và AC → . D B → = 0 thì AD → . B C → = 0 và do đó AD ⊥ BC.”
Giả sử có một mặt cầu tiếp xúc với các cạnh AB, AC, AD, BC, CD, BD của tứ diện ABCD lần lượt tại M, N, P, Q, R, S. Khi đó AM, AN, AP là các tiếp tuyến cùng xuất phát từ A nên AM = AN = AP.
Lập luận tương tự ta có: BM = BQ = BS; CQ = CR = CN; DR = DS = DP
Vậy AB + CD = AM + MB + CR + RD = AN + BS + CN + DS = AN + NC + BS + SD = AC + BD
Bằng lí luận tương tự ta chứng minh được AB + CD = AC + BD = AD + BC