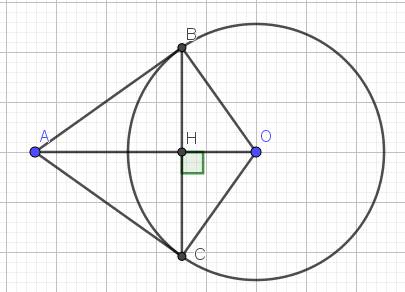
cho (o) và (o') tiếp xúc ngoài tại a. AB là 1 dây của (o), ac là dây của (o') sao cho BAC=90. kẻ ah vuông góc BC. xác định vị trí của ba và ac đê ah lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 5 2020
a) Ta có : \(\widehat{MOA}=\widehat{O_1}'\left(=180^o-2\widehat{A_1}\right)\)
\(\Rightarrow\)O'N // OM
Gọi P là giao điểm của MN và OO'
Ta có : \(\frac{O'P}{OP}=\frac{O'N}{OM}=\frac{R'}{R}\)
gọi P' là giao điểm của BC và OO',ta có :
\(\frac{O'P'}{OP'}=\frac{O'C}{OB}=\frac{R'}{R}\)
Suy ra \(P'\equiv P\)
b) gọi H là hình chiếu của O' trên OM
tứ giác MNO'O là hình thang nên \(S=\frac{\left(OM+O'N\right)O'H}{2}\)
\(S=\frac{R+R'}{2}.O'H\le\frac{R+R'}{2}.OO'=\frac{\left(R+R'\right)^2}{2}\)
Dấu "=" xảy ra khi \(H\equiv O\Leftrightarrow OM\perp OO'\)
Vậy ...
3 tháng 1
Bài 1:
a: Ta có: ΔOBC cân tại O
mà OH là đường cao
nên OH là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
=>\(\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBKD nội tiếp
BD là đường kính
Do đó: ΔBKD vuông tại K
=>BK\(\perp\)KD tại K
=>BK\(\perp\)AD tại K
Xét ΔABD vuông tại B có BK là đường cao
nên \(AK\cdot AD=AB^2\left(1\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AD=AH\cdot AO\)
Câu 8:
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>\(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CBA}=60^0\)
Xét ΔOBC có OB=OC và \(\widehat{OBC}=60^0\)
nên ΔOCB đều
=>BC=OB=R
=>BO=BM=R
=>B là trung điểm của OM
Xét ΔOCM có
CB là đường trung tuyến
CB=1/2OM
Do đó: ΔOCM vuông tại C
b: Ta có: OB+BM=OM
=>OM=R+R=2R
Ta có: ΔOCM vuông tại C
=>\(OC^2+CM^2=OM^2\)
=>\(CM^2=\left(2R\right)^2-R^2=3R^2\)
AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
a. Vì $AB$ là tiếp tuyến của $(O)$ nên $AB\perp BO$. Tức là tam giác $ABO$ vuông tại $B$
$AB=\sqrt{OA^2-OB^2}=\sqrt{5^2-3^2}=4$ (cm)
$\frac{AB}{OA}=\sin \widehat{O_1}=\frac{BH}{BO}$
$\Rightarrow BH=\frac{AB.BO}{OA}=\frac{4.3}{5}=\frac{12}{5}$ (cm)
c.
Vì $BOC$ là tam giác cân tại $O$ (OB=OC=R) nên đường cao $OH$ đồng thời là đường trung trực của $BC$
$A,H,O$ thẳng hàng nên $A$ cũng nằm trên đường trung trực của $BC$
$\Rightarrow AB=AC$
Xét tam giác $ABO$ và $ACO$ có:
$AB=AC$
$BO=CO$
$AO$ chung
$\Rightarrow \triangle ABO=\triangle ACO$ (c.c.c)
$\Rightarrow \widehat{ACO}=\widehat{ABO}=90^0$
$\Rightarrow AC$ là tiếp tuyến của $(O)$
b.
Vì $\triangle ABO=\triangle ACO$ nên $\widehat{BAO}=\widehat{CAO}$
$\Rightarrow \widehat{BAC}=2\widehat{BAO}$
$\sin \widehat{BAO}=\frac{BO}{AO}=\frac{3}{5}$
$\Rightarrow \widehat{BAO}=37^0$
$\Rightarrow \widehat{BAC}=2\widehat{BAO}=2.37^0=74^0$
16 tháng 1 2021
a) Vì đường tròn (O) và (O') tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng.
Ta có: MB = MC (M là TĐ của BC)
Xét (O) ta có: DE vg góc BC (gt)
mà M là TĐ của BC
Suy ra : M là TĐ của DE ( đường kính vuông góc với dây cung)
Xét TG BDCE có 2 đường chéo DE và BC cắt nhau tại trung điểm M của mỗi đường
Suy ra: BDCE là hình bình hành.
16 tháng 1 2021
(Bổ sung)
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi
CM
1 tháng 3 2019
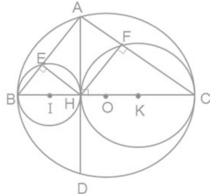
IO = OB – IB => (I) tiếp xúc trong với (O).
OK = OC – KC => (K) tiếp xúc trong với (O)
IK = OH + KH => (I) tiếp xúc ngoài với (K)
