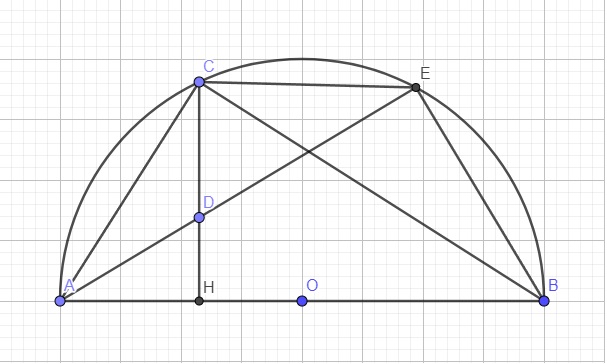
Cho đường tròn tâm (O) đường kính AB. Trên (O) lấy đểm D khác A, B. trên AB lấy điểm C. kẻ CH vuông góc với AD (H thuộc AD). Tia phân giác trong của góc DAB cắt CH tại F và cắt (O) tại E. DF cắt (O) tại N.
a. Chứng minh góc ANF = góc ACF
b. Chứng minh tứ giác FANC nội tiếp.