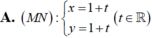
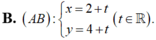
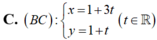
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(S_{ABM}=\dfrac{1}{3}\times S_{ABE}\) (chung đường cao hạ từ \(B\), \(AM=\dfrac{1}{3}\times AE\))
\(\Leftrightarrow S_{ABE}=3\times S_{ABM}=3\times90=270\left(cm^2\right)\)
\(S_{ABE}=\dfrac{1}{3}\times S_{ABC}\) (chung đường cao hạ từ \(A\), \(BE=\dfrac{1}{3}\times BC\))
\(\Leftrightarrow S_{ABC}=3\times S_{ABE}=3\times270=810\left(cm^2\right)\)
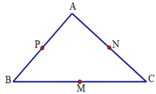
Câu:1 Vì AM=MB , AN=NC
Nên diện tích tam giác AMN=2ABC
=> Diện tích tam gác AMN = 180:2 = 90
a: \(AB=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{\left(5-2\right)^2+\left(3+1\right)^2}=5\)
Do đó: AB=BC
hay ΔABC cân tại B
Kẻ đường cao AH
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
\(S_{ABM}=\dfrac{1}{2}\cdot AH\cdot BM\)
=>\(S_{ABC}=3\cdot S_{ABM}=3\cdot45=135\left(cm^2\right)\)
ta có: AM = 1/2 BC => AM = BM, CM
xét tam giác ABM có : AM = BM
=> ABM cân tại M
xét tam giác ACM có : AM = CM
=> ACM cân tại M
Mà góc AMB + AMC = 180 độ ( kề bù )
=> góc B + góc BAM + góc C + góc CAM = 180 độ
Mà góc B = góc BAM
góc C = góc CAM
=> BAM + CAM = 90 độ
=> tam giác ABC cân tại A
Bài 2:
\(\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{8}{12}=\dfrac{2}{3}\)
=>\(\dfrac{BM}{BC}=\dfrac{2}{3}\)
=>\(BM=\dfrac{2}{3}\cdot BC=\dfrac{2}{3}\cdot24=16\left(cm\right)\)
Ta có: BM+MC=BC
=>MC+16=24
=>MC=8(cm)
