Có bao nhiêu số phức z thỏa mãn ![]() và z2 là số thuẩn ảo.
và z2 là số thuẩn ảo.
A. 2
B. 3
C. 4
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Gọi z = a + bi.
Ta có ![]() và z2 = a2 – b2 + 2abi
và z2 = a2 – b2 + 2abi
Yêu cầu của bài toán thỏa mãn khi và chỉ khi
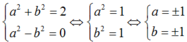
Vậy có 4 số phức thỏa mãn điều kiện bài toán.

Chọn C
Gọi z = x + yix, y ∈ R
![]()
![]()
z2 = (x2 - y2) + 2xyi là số thuần ảo khi và chỉ khi x2 - y2 = 0 (2)
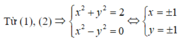
=> Có 4 số phức thỏa yêu cầu đề bài.

Đáp án D.
Đặt z = x + y i , x , y ∈ ℝ ⇒ z = 2 ⇔ x 2 + y 2 = 2 ( 1 )
z 2 = x 2 − y 2 + 2 x y i là số thuần ảo ⇔ x 2 − y 2 = 0 ( 2 ) x y ≠ 0
Từ (1) và (2) ta có hệ x 2 + y 2 = 2 x 2 − y 2 = 0 (ĐK: x y ≠ 0 )
⇔ 2 x 2 = 2 x 2 − y 2 = 0 ⇔ x = 1 x = − 1 y 2 = 1 ⇒ x = 1 y = 1 x = 1 y = − 1 x = − 1 y = 1 x = − 1 y = − 1
Có 4 số phức z thỏa mãn.

Đáp án C
Gọi z=a+bi
![]()
Để ![]() là số thuần ảo
là số thuần ảo
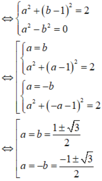
Vậy có 4 số phức thỏa mãn yêu cầu đề bài.
Chọn C.
Đặt z = x + yi
Ta có: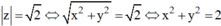
Mặt khác: z2 = ( x + yi) 2 = x2 - y2 + 2xyi là số thuần ảo nên x2 - y2 = 0
Ta có hệ: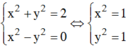
Vậy các số phức cần tìm là: z = 1+ i; z = 1 - i; z = -1 + i và z = -1 - i.