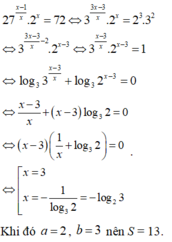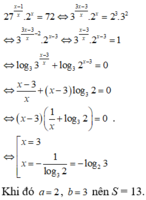Chứng minh rằng số P=4n(a2+b2) luôn viết được dưới dạng m2+n2 với a,b,m,n là các số nguyên dương.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì a,b là các số chẵn nên a,b viết được dưới dạng là a=2m và b=2n(Với m,n∈Z)
Ta có: \(a^2+b^2\)
\(=\left(2m\right)^2+\left(2n\right)^2\)
\(=4m^2+4n^2\)
\(=4\left(m^2+n^2\right)\)
\(=2\left(2m^2+2n^2\right)\)
\(=\left(m^2+n^2+1-m^2-n^2+1\right)\cdot\left(m^2+n^2+1+m^2+n^2-1\right)\)
\(=\left(m^2+n^2+1\right)^2-\left(m^2+n^2-1\right)^2\)
là bình phương của hai số nguyên(đpcm)

Ta có\(33333.....3^2=33333...3\cdot3333....3\)(Mỗi số có n chữ số 3)
=9999...9x1111...1(Mỗi thừa số có n chữ số)
=(10000...01-2)x1111...1(thừa số thứ nhất có n-1 chữ số 0,thừa số thứ hai có n chữ số 1)
=1111....1-2222...2(số bị trừ có 2n chữ số , số trừ có n chữ số)

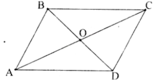
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
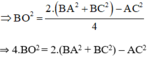
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).