Cho tam giác ABC có góc B tù và đường cao AH.Trên tia AH lấy điểm D sao cho H là trung điểm của AD. chứng minh góc ABC bằng góc DBC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có 3 cách
cách 1

cách 2

cách 3
a) vì A trung điểm DH
E trung điểm HC
=>F là trọng tâm tam giác DHC
=>HF cắt CD tại TĐ K của CD
b) vì F là trọng tâm tam giác HDC nên HF/HK=1/3
mà HK=1/2CD (do tam giác DHC vuông có HK là trung tuyến)
=>HF=1/3 CD

k nha

Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAD cân tại B
Ta có: ΔBAD cân tại B
mà BH là đường cao
nên BH là tia phân giác của góc ABD

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
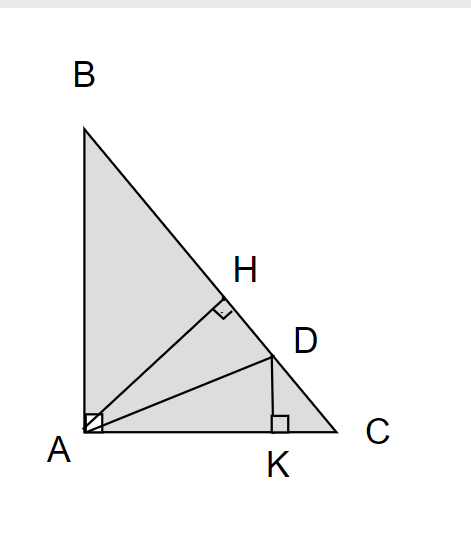
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)


a) \(BEH\)cân tại \(B\)nên \(\widehat{E}=\widehat{H_1}\)
\(\widehat{ABC}=\widehat{E}+\widehat{H_1}=2\widehat{E}\)
\(\widehat{ABC}=2\widehat{C}\)
\(\Rightarrow\widehat{BEH}=\widehat{ACB}\)
b) Chứng minh được \(\Delta DHC\)cân tại \(D\)nên \(DC=DH\)
\(\Delta DHC\)có :
\(\widehat{DAH}=90^0-\widehat{C}\)
\(\widehat{DHA}=90^0-\widehat{H}_2=90^0-\widehat{C}\)
\(\Rightarrow\Delta DAH\)cân tại \(D\)nên \(DA=DH\)
c) \(\Delta ABB'\)cân tại \(A\)nên :
\(\widehat{B'}=\widehat{B}=2\widehat{C}\)
\(\widehat{B'}=\widehat{A_1}+\widehat{C}\)
\(\Rightarrow2\widehat{C}=\widehat{A_1}+\widehat{C}\)
\(\Rightarrow\widehat{C}=\widehat{A_1}\)
\(\Rightarrow\widehat{AB'C}\)cân tại \(B'\)
d) \(AB=AB'=CB'\)
\(BE=BH=B'H\)
Có : \(AE=AB+BE\)
\(HC=CB'+B'H\)
\(\Rightarrow AE=HC\)

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
hình tự vẽ nha bn
tam giac ADC có CH là đường cao đồng thời là trung tuyến ( H là tđ của AD, đường cao AH)
=> tam giac ADC cân tại C
tam giac ADC cân tại C có CH là đường cao => CH là pg=>góc C1=C2
XÉT tam giac ABC và tam giac DBC có
AC=DC,GÓC C1=C2,BC CẠNH CHUNG
=> tam giac ABC=tam giac DBC (C-G-C)
=> GÓC ABC=GÓC DBC