K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
3 tháng 12 2017
Tính đạo hàm của hàm số 2 x + 3                                     k h i   x ≥ 1 x 3 + 2 x 2 - 7 x + 4 x - 1   k h i   x < 1   tại x 0 = 1 . A. 0 B. 4 C. 5...
Đọc tiếp

Tính đạo hàm của hàm số 2 x + 3                                     k h i   x ≥ 1 x 3 + 2 x 2 - 7 x + 4 x - 1   k h i   x < 1   tại x 0 = 1 .

A. 0

B. 4

C. 5

D. Đáp án khác 
#Toán lớp 11
1
CM
Cao Minh Tâm
3 tháng 12 2017

Đáp án D

Đúng(0)
PT
Pham Trong Bach
3 tháng 2 2017

Tính đạo hàm của hàm số: y   =   tan   π / 2   –   x với x   ≠   k π ,   k   ∈   Z

#Toán lớp 11
1
CM
Cao Minh Tâm
3 tháng 2 2017

Đặt u = π/2 - x thì u' = -1

Giải bài tập Toán 11 | Giải Toán lớp 11

Do cos⁡(π/2-x) = sin⁡x

Đúng(0)
PT
Pham Trong Bach
10 tháng 7 2019
Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt h x = f x g x . Tính h' (2) đạo hàm của hàm số h(x) tại x = 2. A.  h ' 2 = 4 49 B.  h ' 2 = - 4 49 C.  h ' 2 = 2 7 D. h ' 2 = - 2 7 ...
Đọc tiếp

Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt h x = f x g x . Tính h' (2) đạo hàm của hàm số h(x) tại x = 2.

A.  h ' 2 = 4 49

B.  h ' 2 = - 4 49

C.  h ' 2 = 2 7

D. h ' 2 = - 2 7  
#Mẫu giáo
1
CM
Cao Minh Tâm
10 tháng 7 2019

Đáp án B

Đúng(0)
PT
Pham Trong Bach
23 tháng 3 2017

Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt  h ( x ) = f ( x ) g ( x ) . Tính h'(2) đạo hàm của hàm số h(x) tại x = 2.

A. 4/49

B. -4/49

C. 2/7

D. -2/7
#Toán lớp 12
1
CM
Cao Minh Tâm
23 tháng 3 2017

Đúng(0)
NH
Nguyễn Hải Vân
19 tháng 4 2021
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm...
Đọc tiếp

Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:

a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)

b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)

Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:

a) \(y=f(2-3x)\)

b) \(y=f(x^2+1)\)

c) \(y=f(3x+1)\)
#Toán lớp 12
0
PT
Pham Trong Bach
10 tháng 8 2019
Cho hàm số y=f(x) có đạo hàm liên tục trên − 1 ; 2 . Đồ thị của hàm số y=f'(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f − 1 = 19 12 , tính f(2). A.  f 2 = 23 6 . B.  f 2 = − 2 3 . C.  f 2 = 2 ...
Đọc tiếp

Cho hàm số y=f(x) có đạo hàm liên tục trên − 1 ; 2 . Đồ thị của hàm số y=f'(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f − 1 = 19 12 , tính f(2).

A.  f 2 = 23 6 .

B.  f 2 = − 2 3 .

C.  f 2 = 2 3 .

D.  f 2 = 11 6 .

#Mẫu giáo
2
CM
Cao Minh Tâm
10 tháng 8 2019

Đáp án B

Đúng(0)
N
nice
10 tháng 8 2022

B 

 

Đúng(0)
PT
Pham Trong Bach
8 tháng 5 2018
Cho hàm số y =f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y = f'(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là 5 12  và  8 3 . Biết f - 1 = 19 12 ,  tính f(2) A. f 2   =   - 2 3   B. f 2   =   2 3   C. f 2   =   11 6   D. ...
Đọc tiếp

Cho hàm số y =f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y = f'(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là 5 12  và  8 3 . Biết f - 1 = 19 12 ,  tính f(2)

A. f 2   =   - 2 3  

B. f 2   =   2 3  

C. f 2   =   11 6  

D. f 2   =   3  
#Mẫu giáo
1
CM
Cao Minh Tâm
8 tháng 5 2018

Dựa vào đồ thị ta thấy: 

Mặt khác: 

Từ đó suy ra 

Chọn A.

Đúng(0)
B
Buddy
17 tháng 8 2023

Tính đạo hàm của các hàm số sau:

a) \(y = {x^2} + 1;\)                       

b) \(y = kx + c\) (với k, c là các hằng số).
#Toán lớp 11
1
NL
Nguyễn Lê Phước Thịnh
18 tháng 8 2023

a: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{x^2+1-x_0^2-1}{x-x_0}\)

\(=\lim\limits_{x\rightarrow x0}\dfrac{\left(x-x0\right)\left(x+x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}x+x0=x0+x0=2x0\)

b: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}\)

\(=\lim\limits_{x\rightarrow x0}\dfrac{kx+c-k\cdot x0-c}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{k\left(x-x0\right)}{x-x0}\)

=\(\lim\limits_{x\rightarrow x0}k=k\)

 

 

Đúng(1)
PT
Pham Trong Bach
13 tháng 9 2018
Hàm số y = f(x) có đạo hàm trên R \ { -2; 2}, có bảng biến thiên như sau: Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f ( x ) - 2018 . Tính k + l A.  . B.  . C.  . D. ...
Đọc tiếp

Hàm số y = f(x) có đạo hàm trên R \ { -2; 2}, có bảng biến thiên như sau:

Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f ( x ) - 2018 . Tính k + l

A.  .

B.  .

C.  .

D.  .
#Toán lớp 12
1
CM
Cao Minh Tâm
13 tháng 9 2018

Đáp án C

Vì phương trình có ba nghiệm phân biệt nên đồ thị hàm số 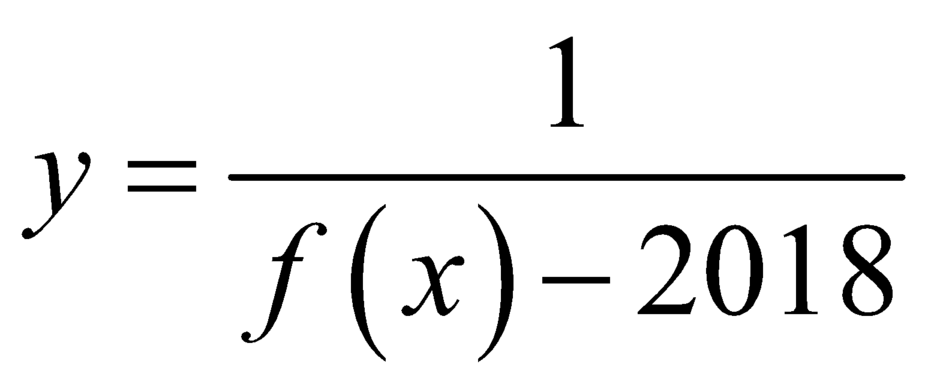có ba đường tiệm cận đứng.

Mặt khác, ta có:

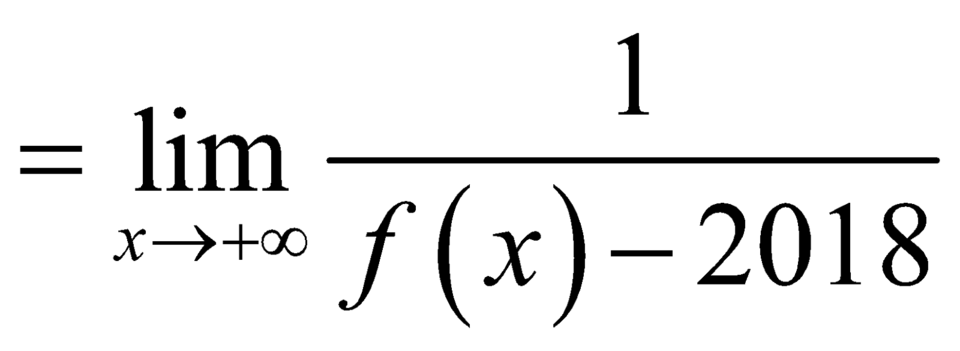
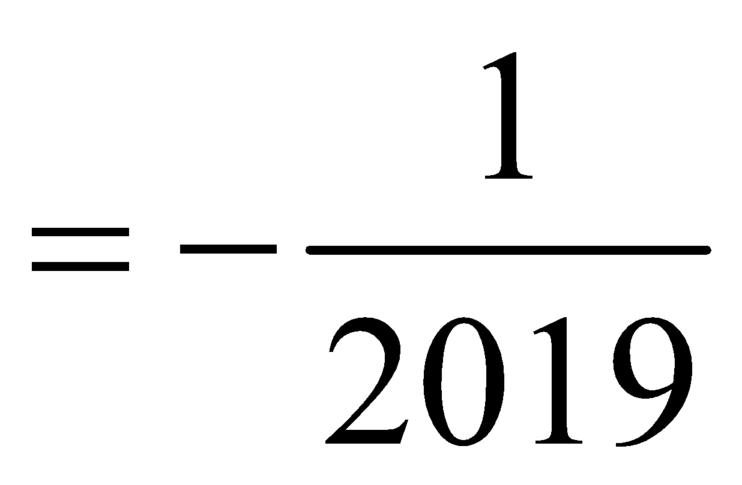nên đường thẳng là đường tiệm cận ngang của đồ thị hàm số .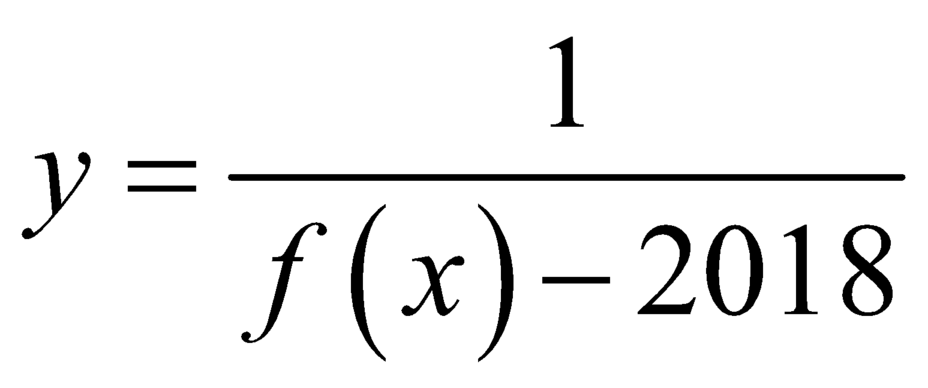

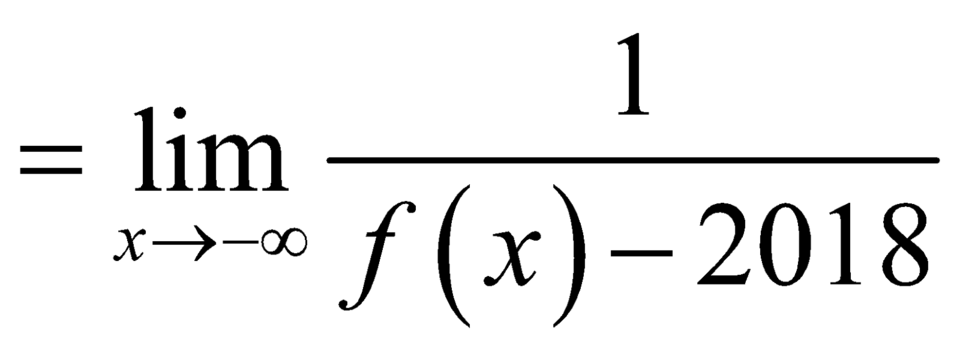
Và nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số .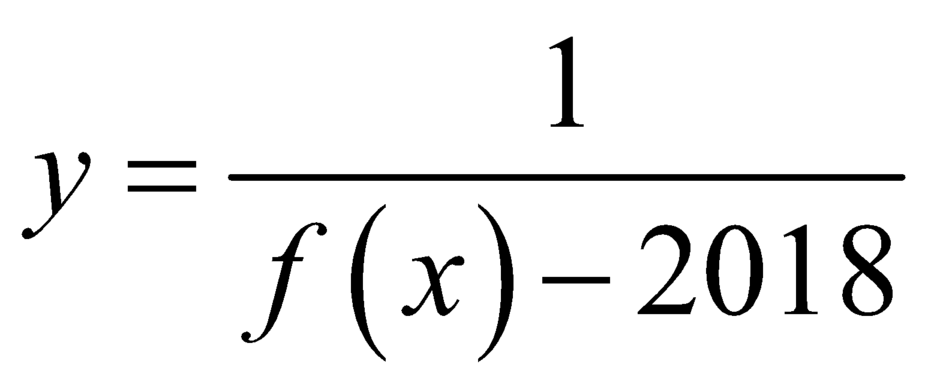

Vậy .

Đúng(0)
NK
Nguyễn Kiều Anh
30 tháng 7 2021

1. Đạo hàm của hàm số y= \(\left(x^3-5\right).\sqrt{x}\) bằng bao nhiêu?

2. Đạo hàm của hàm số y= \(\dfrac{1}{2}x^6-\dfrac{3}{x}+2\sqrt{x}\) là?

3. Hàm số y= \(2x+1+\dfrac{2}{x-2}\) có đạo hàm bằng?
#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021

1. \(y'=3x^2\sqrt{x}+\dfrac{x^3-5}{2\sqrt{x}}=\dfrac{7x^3-5}{2\sqrt{x}}\)

2. \(y'=3x^5+\dfrac{3}{x^2}+\dfrac{1}{\sqrt{x}}\)

3. \(y'=2-\dfrac{2}{\left(x-2\right)^2}\)

Đúng(1)
T
títtt
15 tháng 9 2023

1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)

2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)

3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
#Toán lớp 11
2
ND
Nguyễn Đức Trí
15 tháng 9 2023

1) \(f\left(x\right)=2x-5\)

\(f'\left(x\right)=2\)

\(\Rightarrow f'\left(4\right)=2\)

2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)

\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)

3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)

\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)

\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)

Đúng(3)
NL
Nguyễn Lê Phước Thịnh
15 tháng 9 2023

loading...  loading...  

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP