Ai giải giúp mình với gấp lắm ạ

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

\(P=\left[\dfrac{x\left(x-2\right)}{2\left(x^2+4\right)}-\dfrac{2x^2}{\left(2-x\right)\left(x^2+4\right)}\right]\cdot\dfrac{x^2-x-2}{x^2}\\ P=\dfrac{-x\left(x-2\right)^2-4x^2}{2\left(x^2+4\right)\left(2-x\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\\ P=\dfrac{x^3+4x}{2\left(x^2+4\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\\ P=\dfrac{x\left(x^2+4\right)\left(x+1\right)}{2x^2\left(x^2+4\right)}=\dfrac{x+1}{2x}\)

Điều kiện: \(n\ge3\)
Giả thiết tương đương:
\(\dfrac{n!}{\left(n-3\right)!.3!}-\dfrac{\left(n-1\right)!}{2!\left(n-3\right)!}=\dfrac{\left(n-1\right)!}{\left(n-2\right)!}.\dfrac{\left(n+3\right)!}{\left(n+2\right)!}\)
\(\Leftrightarrow\dfrac{n\left(n-1\right)\left(n-2\right)}{6}-\dfrac{\left(n-1\right)\left(n-2\right)}{2}=\left(n-1\right)\left(n+3\right)\)
\(\Leftrightarrow\dfrac{n\left(n-2\right)}{6}-\dfrac{n-2}{2}=n+3\)
\(\Leftrightarrow n^2-11n-12=0\Rightarrow\left[{}\begin{matrix}n=12\\n=-1\left(loại\right)\end{matrix}\right.\)
Vậy khai triển đã cho là: \(x^3\left(x^3-\dfrac{12}{3x}\right)^{12}=x^3\left(x^3-\dfrac{4}{x}\right)^{12}\)
Số hạng tổng quát trong khai triển:
\(C_{12}^k.\left(x^3\right)^k.\left(-\dfrac{4}{x}\right)^{12-k}.x^3=C_{12}^k.\left(-4\right)^{12-k}.x^{4k-9}\)
Số hạng chứa \(x^{11}\) thỏa mãn:
\(4k-9=11\Leftrightarrow k=5\)
Hệ số: \(C_{12}^5.\left(-4\right)^7=-C_{12}^5.4^7=...\)

Gọi gốc là điểm A, chỗ gãy là B, ngọn đã gãy là điểm C
Xét tam giác ABC vuông tại A có: AB = 6m, BC = 16m - 6m = 10m
=> AB2 + AC2 = BC2 (Định lý Py-ta-go)
Thay: 62 + AC2 = 102
36 + AC2 = 100
AC2 = 100 - 36 = 64
AC = 8 (m)
Vậy khoảng cách từ gốc đến ngọn cây bị gãy là 8 mét
Nếu đúng hãy K cho mình nha
Học tốt nhé

a) \(d\left(A;\Delta\right)=\dfrac{\left|4.1-3.3+2\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{3}{5}\)
b) \(\overrightarrow{AB}=\left(-3;-2\right)\) là VTCP của đường thẳng d
PT tham số của d: \(\left\{{}\begin{matrix}x=1-3t\\y=3-2t\end{matrix}\right.\left(t\in R\right)\)
c) Đường tròn (C) có bán kính \(R=AB=\sqrt{\left(1+2\right)^2+\left(3-1\right)^2}=\sqrt{13}\)
PT đường tròn (C): \(\left(x-1\right)^2+\left(y-3\right)^2=13\)

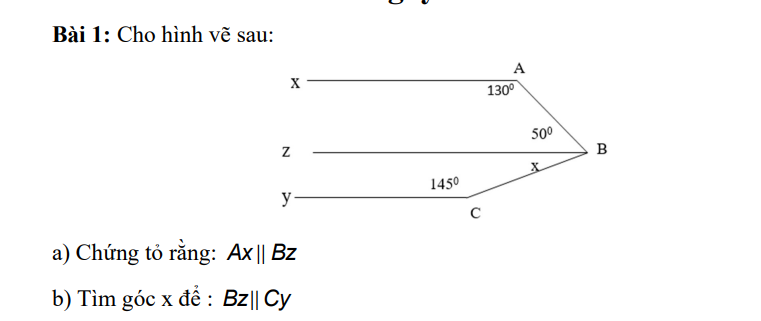
\(\widehat{XAB}\) + \(\widehat{ABZ}\) = 1300 + 500 = 1800
Vì góc XAB và góc ABZ là hai góc trong cùng phía nên
Ax // BZ
BZ // Cy ⇔ \(x\) + \(\widehat{yCB}\) =1800
⇒ \(x\) = 1800 - 1450 = 350

2:
a: pi/2<a<pi
=>cosa<0
sin^2a+cos^2a=1
=>cos^2a=1-4/9=5/9
=>cosa=-căn 5/3
cos2a=2*cos^2a-1=2*5/9-1=10/9-1=1/9
sin(2a-pi/6)
=sin2a*cospi/6-cos2a*sinpi/6
=2*sina*cosa*(căn 3/2)-1/9*1/2
\(=2\cdot\dfrac{2}{3}\cdot\dfrac{-\sqrt{5}}{3}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{1}{18}=\dfrac{-4\sqrt{15}-1}{18}\)
b; tan a=2
=>sin a=2*cosa
\(A=\dfrac{3\cdot\left(2\cdot cosa\right)^2-cos^2a+2}{5\cdot\left(2\cdot cosa\right)^2+3cosa\cdot2cosa}\)
\(=\dfrac{12\cdot cos^2a-cos^2a+2}{20cos^2a+6cos^2a}\)
\(=\dfrac{11cos^2a+2\left(4cos^2a+cos^2a\right)}{26cos^2a}=\dfrac{21}{26}\)
4:
a: (C): x^2+y^2-4x+2y-4=0
=>x^2-4x+4+y^2+2y+1=9
=>(x-2)^2+(y+1)^2=9
=>I(2;-1); R=3
b: Gọi (d) là phương trình cần tìm
(d)//4x+3y-1=0
=>(d): 4x+3y+c=0
I(2;-1);R=3
Theo đề, ta có: d(I;(d))=R=3
=>\(\dfrac{\left|4\cdot2+3\cdot\left(-1\right)+c\right|}{\sqrt{4^2+3^2}}=3\)
=>|c+5|=15
=>c=10 hoặc c=-20


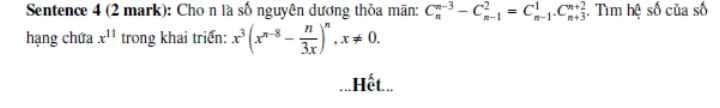


 ai làm giúp mình với mình đang cần gấp lắm ạ
ai làm giúp mình với mình đang cần gấp lắm ạ
