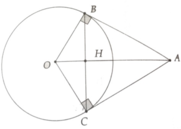
cho (O), A là 1 điểm nằm ngoài đường tròn, qua A kẻ các tiếp tuyến AB và AC . a) CM OA vuông góc BC.b) Gọi I là giao điểm của AO với (O), CM OI là tia phân giác của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2023
a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
=>ΔABC cân tại A
b: OB=OC
AB=AC
Do đó: AO là trung trực của BC
=>AO vuông góc với BC
CM
3 tháng 11 2017
a, HS tự làm
b,i, Áp dụng định lý Pytago tính được BH = 3 cm
Áp dụng hệ thức lược về cạnh góc vuông và đường cao trong tam giác vuông, tính được:
AB = AC = 2 3 cm => P A B C = 6 3 cm, S A B C = 3 3 c m 2
ii, Ta có: S A B O C = S A B C + S B O C = 4 3 c m 2
22 tháng 12 2018
a, Vì OB = OC ( =R )
AB = AC (tiếp tuyến)
=> OA là trung trực BC
=> OA vuông góc BC
Vì AB là tiếp tuyến (O)
\(\Rightarrow OB\perp AB\)
=> t/g OAB vuông tại B
Xét t/g OAB vuông tại B có BH là đường cao
=>\(OH.OA=OB^2=R^2\)(hệ thức lượng)
b,* Xét \(\Delta\)BCD có : OB = OC = OD (=R)
=> \(\Delta\)BCD vuông tại C
=> \(BC\perp CD\)
Mà \(BC\perp OA\)
=> CD // OA
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC