Trong hình bs 11 ta có tam giác EFG và tia Fm.
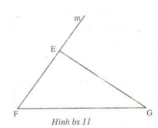
Chứng minh rằng ∠GEm =∠ EFG + ∠EGF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


EFG
+
EGF
=
GEm
suy ra G+F=m dư 1
m+1=E
mình nói đến đây thôi nha vì mình học lớp 6

Tổng 3 góc tam giác = 180 độ => góc FEG = 180 độ - FEG - EGF
Mà FEG và GEm bù nhau => FEG = 180 độ - GEm => EFG + EGF = GEm

Gọi x là cạnh của hình vuông ABCD.
Theo đề bài, diện tích phần tô đen bằng 4/5 diện tích tam giác EFG và bằng 12 diện tích của hình vuông ABCD. Ta có phương trình:
4/5 * 40 = 12 * x^2
32 = 12 * x^2
2.67 = x^2
Vậy, x = √2.67
Đáp án: độ dài cạnh của hình vuông ABCD là khoảng 1.63 cm (làm tròn đến hai chữ số thập phân)

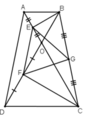

ΔAOB đều ⇒ BE là đường trung tuyến đồng thời là đường cao
⇒ BE ⊥ AO
⇒ ΔBEC vuông tại E
Mà EG là đường trung tuyến
⇒ 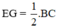 (1)
(1)
ΔCOD đều ⇒ CF là đường trung tuyến đồng thời là đường cao
⇒ CF ⊥ OD
⇒ ΔBFC vuông tại F
Mà FG là đường trung tuyến
⇒ 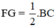 (2)
(2)
Hình thang ABCD (AB// CD) có: AC = AO + OC = OB + OD = BD
⇒ ABCD là hình thang cân
⇒ AD = BC.
ΔAOD có: AE = EO, FO = FD
⇒ EF là đường trung bình của ΔAOD
⇒ 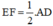
Mà AD = BC (cmt)
⇒ 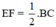 (3)
(3)
Từ (1); (2); (3) suy ra EF = FG = GE ⇒ ΔEFG đều (đpcm).
Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.