Hàm số y = x + 2 x 2 + 1 có bao nhiêu cực trị?
A. 0
B. 1
C. 2
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án: B.
Hàm số y = ( x + 1 ) 3 (5 - x) xác định trên R.
y' = - ( x + 1 ) 3 + 3 ( x + 1 ) 2 (5 - x) = 2 ( x + 1 ) 2 (7 - 2x)
y' = 0 ⇔ 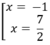
Bảng biến thiên
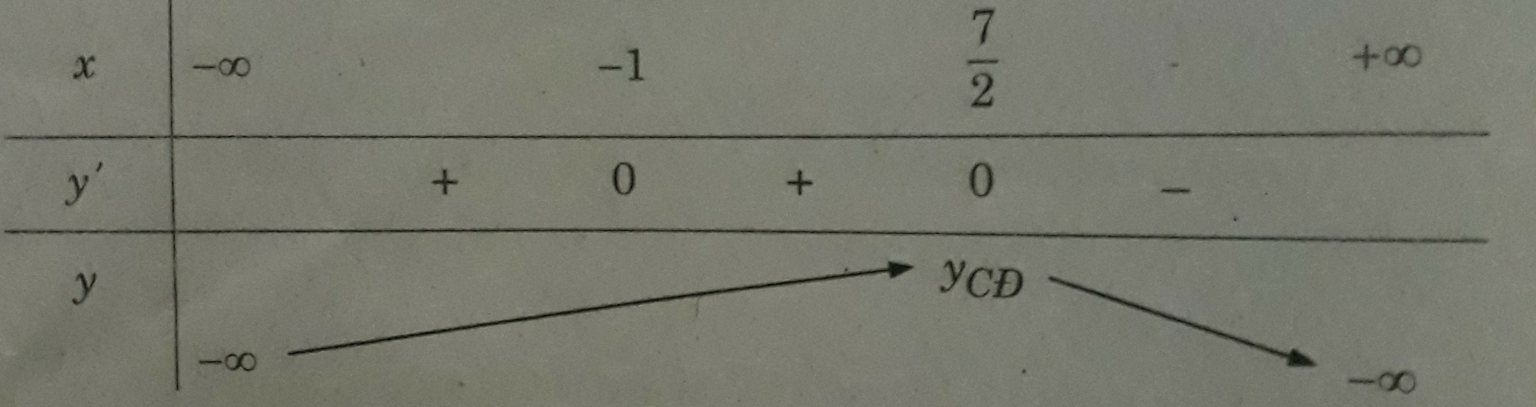
Suy ra hàm số chỉ có một cực trị (là cực đại)
Cách khác: Nhận xét rằng y' chỉ đổi dấu khi x đi qua 7/2 nên hàm số chỉ có một cực trị

Đáp án A.
Đặt u = x 2 - 2 x , ta có y = f u ⇒ y ' = 2 x - 2 f ' u = 2 x - 2 f ' x 2 - 2 x .
Do đó, phương trình y ' = 0 ⇔ [ 2 x - 2 = 0 x 2 - 2 x = - 2 x 2 - 2 x = - 1 x 2 - 2 x = 0 ⇔ [ x - 1 3 = 0 x 2 - 2 x + 2 = 0 x 2 - 2 x = 0 ⇔ [ x = 0 x = 1 x = 2 .
Vậy hàm số đã chốc 3 điểm cực trị là x = 0; x= 1; x = 2.

Đáp án B
Hàm số y = x + 1 3 (5 - x) xác định trên R.
y' = - x + 1 3 + 3 x + 1 2 (5 - x) = 2 x + 1 2 (7 - 2x)
y' = 0 ⇔ 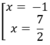
Bảng biến thiên
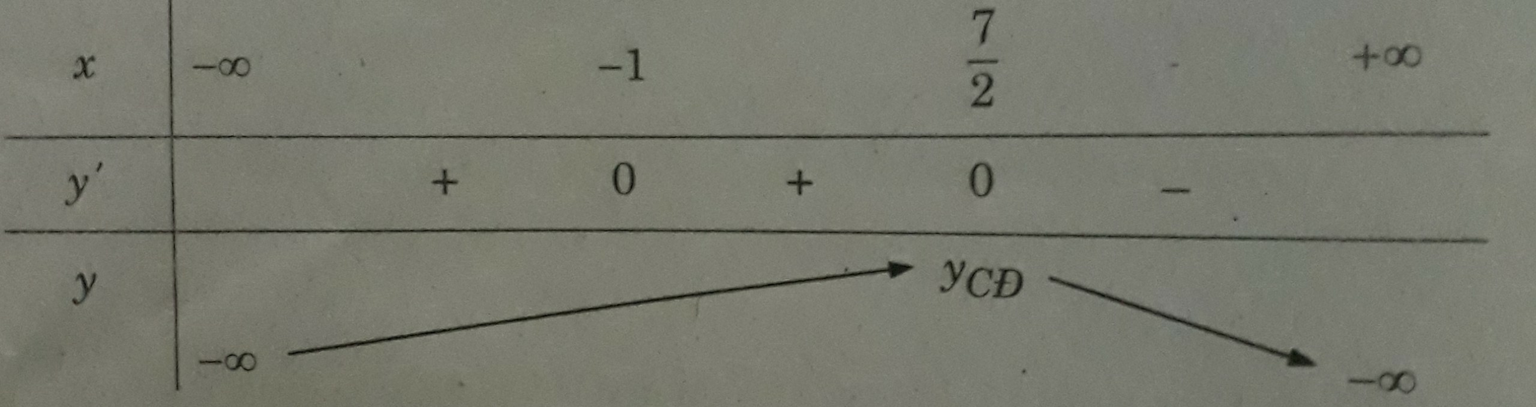
Suy ra hàm số chỉ có một cực trị (là cực đại)
Cách khác: Nhận xét rằng y' chỉ đổi dấu khi x đi qua 7/2 nên hàm số chỉ có một cực trị

\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
đơn điệu trên R là sao bạn? bạn chỉ mk cách nhận bt đc ko?

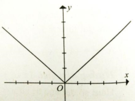
Đồ thị hàm số y = |x| có dạng hình vẽ.
Từ đồ thị trong hình ta có hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó. Sử dụng định nghĩa cực trị ta có hàm số y = |x| đạt cực tiểu tại x = 0
Do đó mệnh đề 1 và 4 đúng. Chọn đáp án C

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 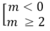

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 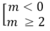
Đáp án đúng : B