Cho có hai đỉnh B, C cố định còn đỉnh A chạy trên một đường tròn ( O:R ). Tìm quỹ tích trọng tâm G của ∆ A B C
A. Đường tròn O ; 1 3 R là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 1 3
B. Đường tròn O ; 2 3 R là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 2 3
C. Đường tròn O ; 4 3 R là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 4 3
D. Đường tròn ( O;3R ) là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 3

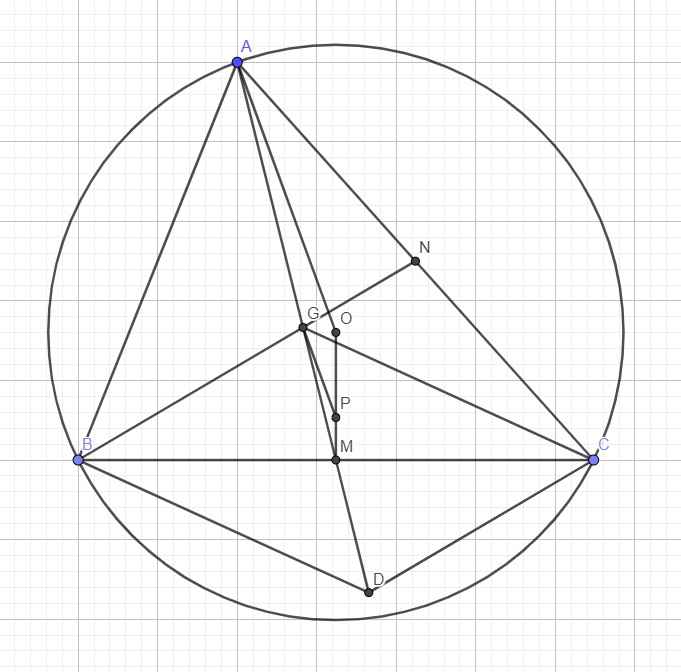
Gọi I là trung điểm BC. Khi đó I G = 1 3 I A ⇒ G = V I ; 1 3
Mà A ∈ O ; R nên quỹ tích trọng tâm G của ∆ A B C là đường tròn O ; 1 3 R là ảnh của đường tròn ( O;R ), qua phép vị tự tâm I tỉ số k = 1 3
Đáp án A