Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2MC. Mệnh đề nào sau đây đúng?
A. M G | | B C D
B. M G | | A C D
C. M G | | A B D
D. M G | | A B C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi N là trung điểm của AD
G là trọng tâm của tam giác ABD nên:

⇒ MG // CN.
Do CN thuộc (ACD) nên MG // (ACD).
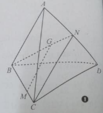
Đáp án A

Đáp án C
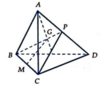
Gọi P là trung điểm của AD
![]()
=> MG // CP => MG // (ACD)

Đáp án D
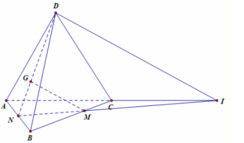
Gọi N là trung điểm của AB.Trong mặt phẳng (ABC)
gọi I là giao điểm của MN và AC.Ta có N G N D = N M N I = 1 3 ⇒ G M / / D I
Mà D I ⊂ A C D ⇒ G M / / A C D .

\(BG\) cắt \(AD\) tại \(K\), \(BM\) cắt \(AC\) tại \(C\).
Giao tuyển của hai mặt phẳng \(\left(BGM\right)\) và \(\left(ACD\right)\) là \(CK\).
Đáp án B
Lấy điểm N trên cạnh BD sao cho NB = 2ND. Khi đó ta có M N | | D C .
Gọi I là trung điểm BD ta có G ∈ A I và I G = 1 3 I A .
Mặt khác ta có D N = 1 3 D B = 2 3 D I ⇒ I N = 1 3 I D .
Từ (2) và (3) suy ra N G | | A D .
Từ (1) và (4) suy ra G M N | | A C D do đó G M | | A C D
Nhận xét: Có thể loại các đáp án sai bằng cách nhận xét đường thẳng GM cắt các mặt phẳng (BCD), (ABD), (ABC).