Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)

Trong (BCD): DG BC = F
Vậy DG (ABC) = F.
b. Cách 1: MG (BMG) (ABH) (H = BG DC)
(Do mặt phẳng (BMG) "lơ lửng" trong hình chóp nên ta kéo dài BM thành BA và BG thành BH để ta có cái nhìn dễ dàng hơn đối với mặt phẳng này).
(BMG) (ACD) =AH
Trong (ABH): MG AH =K
Vậy MG (ACD) = K.
a. Trong (BCD) có GD và BC cắt nhau tại K
vậy K = GD và (ABC)
b. có MG ⊂ (BMG) trùng (ABH) có H = BG và DC
(BMG) và (ACD) = AH
Trong (ABH) có MG và AH = P
Vậy MG và (ACD) = P

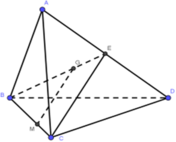
Gọi E là trung điểm của AB, M, N lần lượt là trọng tâm của các tam giác ABC, ABD nên:
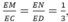
Theo định lí Ta – lét ta có: MN // CD. Vậy MN // (BCD), MN // (ACD).
Đáp án C.

Đáp án C
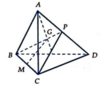
Gọi P là trung điểm của AD
![]()
=> MG // CP => MG // (ACD)

Gọi E là trung điểm của AB. M, N lần lượt là trọng tâm các tam giác ABC, ABD nên:
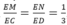
Theo định lí Ta – lét ta có MN // CD.
Đáp án A

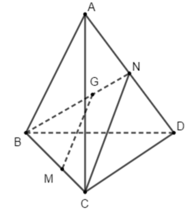
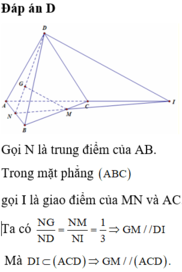
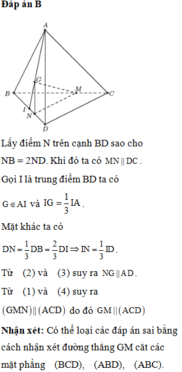
Gọi N là trung điểm của AD
G là trọng tâm của tam giác ABD nên:
⇒ MG // CN.
Do CN thuộc (ACD) nên MG // (ACD).
Đáp án A