Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

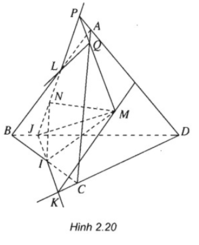
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
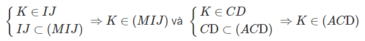
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
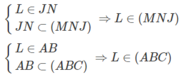
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
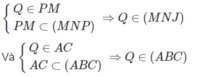
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).

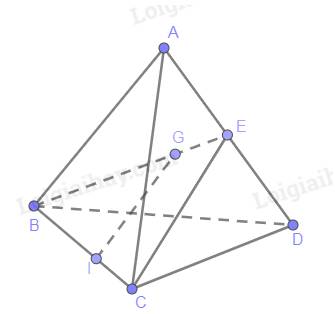
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)

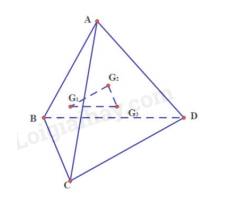
a) Gọi E, F, H là trung điểm của BC, CD, BD
Ta có:\({G_1}\) là trọng tâm tam giác ABC, suy ra\(\frac{{A{G_1}}}{{AE}} = \frac{2}{3}\)
\({G_3}\)là trọng tâm tam giác ABD, suy ra\(\frac{{A{G_3}}}{{AH}} = \frac{2}{3}\)
Suy ra tam giác AEH có\(\frac{{A{G_1}}}{{AE}} = \frac{{A{G_3}}}{{AH}}\) nên \({G_1}{G_3}//EH\)
Mà EH thuộc (BCD) nên \({G_1}{G_3}//(BCD)\)
Tương tự ta có:\({G_2}{G_3}//(BCD)\)
Do đó, \({G_1}{G_2}{G_3}//(BCD)\)
b) Ta có: \({G_1}{G_2}{G_3}//(BCD)\) nên \({G_1}{G_2} // BD\)
mà \({G_3}\) là điểm chung của hai mặt phẳng
Từ \({G_3}\) kẻ \({G_3}x\) sao cho \({G_3}x//BD\)
Vậy \({G_3}x\) là giao tuyến cần tìm.
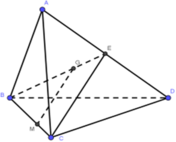

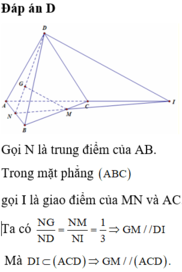



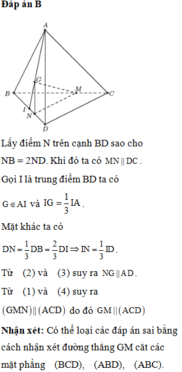
\(BG\) cắt \(AD\) tại \(K\), \(BM\) cắt \(AC\) tại \(C\).
Giao tuyển của hai mặt phẳng \(\left(BGM\right)\) và \(\left(ACD\right)\) là \(CK\).