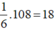Trong không gian Oxyz, mặt phẳng (α) đi qua M (1;1;4) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C phân biệt sao cho tứ diện OABC có thể tích nhỏ nhất. Tính thể tích nhỏ nhất đó.
A. 72.
B. 108
B. 18.
D. 36.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 1 2020
Đáp án A
Phương trình mặt phẳng (α): 2(x - 1) + 3(y + 2) + 5(z - 4)=0<=> 2x + 3y + 5z - 16=0.
CM
8 tháng 5 2019
Đáp án C
Phương pháp:
+) Phương trình đường thẳng đi điểm M ( x 0 ; y 0 ; z 0 ) và có VTPT n → = ( a ; b ; c ) có phương trình:
+) Hai vecto u → , v → cùng thuộc một mặt phẳng thì mặt phẳng đó có VTPT là: n → = u → , v →
Cách giải:
Mặt phẳng ( α ) chứa điểm M và trục Ox nên nhận n α → = O M → , u O x → là một VTPT.
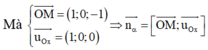
Kết hợp với ( α ) đi qua điểm M(1;0;-1)
CM
6 tháng 8 2018
Đáp án C.
Mặt phẳng α nhận O M → ; u Ox → là một VTPT.
Mà O M → = 1 ; 0 ; − 1 u O x → = 1 ; 0 ; 0
⇒ O M → ; u Ox → = 0 ; − 1 ; 0 .
Kết hợp với α đi qua M(1;0;-1)
⇒ α : − y − 0 = 0 ⇔ y = 0.
CM
12 tháng 4 2017
Đáp án C
Phương trình mặt phẳng qua M và song song với ( α ) là:
3(x-3)-(y+1)+2(z+2)=0 ⇔ 3x-y+2z-6=0
Chọn B
Đặt A= (a;0;0), B= (0;b;0), C= (0;0;c) với a, b, c>0.
Khi đó phương trình mặt phẳng (α) là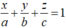
Vì (α) đi qua M (1;1;4) nên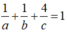
Thể tích của tứ diện OABC là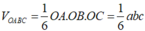
Áp dụng bất đẳng thức AM - GM ta có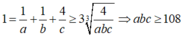
Dấu bằng xảy ra khi a=b=3 ; c=12.
Vậy tứ diện OABC có thể tích nhỏ nhất bằng