Không vẽ hình, hãy cho biết hệ phương trình sau có bao nhiêu nghiệm.
x − 2 y + 10 = 0 − 3 x + 6 y − 30 = 0
A. 1
B. Vô số
C. 0
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 3 2017
Đáp án A
+ Tập nghiệm của phương trình y = 2x + 10 được biểu diễn bởi đường thẳng d 1 :y = 2x + 10.
+ Tập nghiệm của phương trình y = x + 100 được biểu diễn bởi đường thẳng d 2 : y = x + 100.
Lại có: hệ số góc của hai đường thẳng d 1 ; d 2 khác nhau (2 ≠ 1) nên hai đường thẳng này cắt nhau.
Suy ra, hệ phương trình đã cho có nghiệm duy nhất.
CM
28 tháng 3 2019
Ta có |f(x)|=10/3→f(x)=10/3 hoặc f(x)= -10/3
Từ bảng biến thiên ta thấy:
Phương trình f(x)=10/3 có 3 nghiệm phân biệt.
Phương trình f(x)= -10/3 có 1 nghiệm
Vậy phương trình đã cho có 4 nghiệm.
Đáp án D
CM
7 tháng 11 2017
Đáp án D
Ta có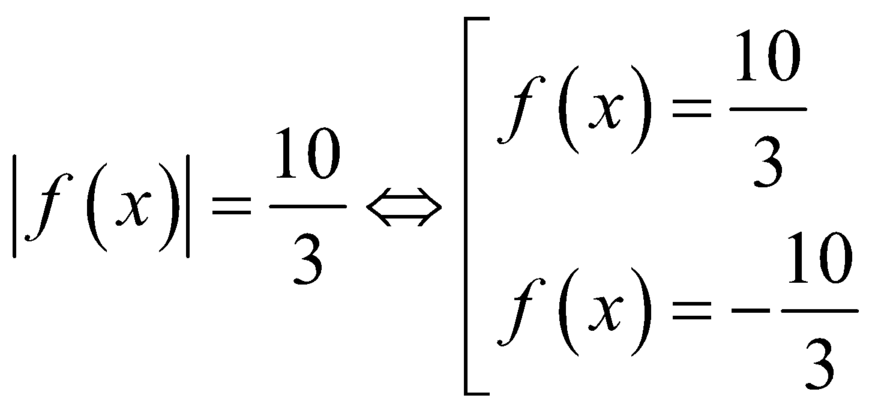 
Từ bảng biến thiên ta thấy:
Phương trình 
có 3 nghiệm phân biệt.
Phương trình 
có 1 nghiệm
Vậy phương trình đã cho có 4 nghiệm
CM
22 tháng 7 2017
Hệ tương đương với x y x + y x + y + x y = 30 x y x + y + x + y + x y = 11
Đặt xy (x + y) = a; xy + x + y = b. Ta thu được hệ:
a b = 30 a + b = 11 ⇔ a = 5 ; b = 6 a = 6 ; b = 5 ⇔ x y x + y = 5 x y + x + y = 6 x y x + y = 6 x y + x + y = 5
TH1: x y x + y = 6 x y + x + y = 5
⇔ x y = 2 x + y = 3 x y = 3 x + y = 2 ( L ) ⇔ x = 2 ; y = 1 x = 1 ; y = 2
TH2: x y x + y = 5 x y + x + y = 6
⇔ x y = 5 x + y = 1 L x y = 1 x + y = 5 ⇔ x = 5 − 21 2 ; y = 5 + 21 2 x = 5 + 21 2 ; y = 5 − 21 2
Vậy hệ có nghiệm (x; y) = (1; 2), (2; 1), 5 ± 21 2 ; 5 ∓ 21 2
Suy ra có một cặp nghiệm thỏa mãn đề bài là 5 − 21 2 ; 5 + 21 2
Đáp án:D
CM
3 tháng 3 2019
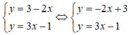
Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ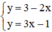 
có nghiệm duy nhất.
CM
5 tháng 9 2019
x = 2 2 x - y = 3
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
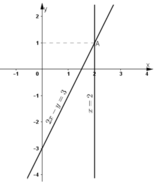
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
CM
3 tháng 9 2017
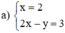
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
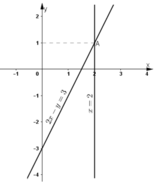
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
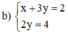
Đường thẳng (d): x + 3y = 2 không song song với trục hoành
Đường thẳng (d’): 2y = 4 hay y = 2 song song với trục hoành
⇒ (d) cắt (d’)
⇒ Hệ phương trình có nghiệm duy nhất.
Vẽ (d1): x + 3y = 2
- Cho y = 0 ⇒ x = 2 được điểm (2; 0).
- Cho x = 0 ⇒ y =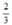 
được điểm (0; 
).
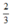Vẽ (d2): y = 2 là đường thẳng đi qua (0; 2) và song song với trục hoành.
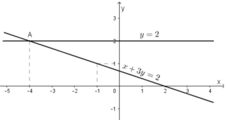
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(-4; 2).
Vậy hệ phương trình có nghiệm (-4; 2).
Đáp án B
Ta có:
Nên tập nghiệm của phương trình x – 2y + 10 = 0 được biểu diễn bởi đường thẳng (d1):
Nên tập nghiệm của phương trình -3x +6y – 30= 0 được biểu diễn bởi đường thẳng (d2):
Do đó, nên hệ phương trình đã cho có vô số nghiệm.