Xét dấu tam thức bậc hai: x2 + 12x + 36
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 6 2018
a) \(f\left(x\right)=5x^2-3x+1\text{ có }\Delta=9-20=-11< 0\text{ và có Hsố là: }a=5>0\text{ nên }f\left(x\right)>0;\forall x\inℝ\)
b) \(f\left(x\right)=-2x^2+3x+5\text{ có }\Delta=9+40=49\)
Tam thức có hai nghiệm phân biệt: \(\orbr{\begin{cases}x_1=-1\\x_2=\frac{5}{2}\end{cases}}\)
Ta có bảng xét dấu:
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left\{-1;\frac{5}{2}\right\}\)
\(f\left(x\right)=0\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{5}{2}\end{cases}}\)
\(f\left(x\right)< 0\Leftrightarrow x\in\left\{-\infty;-1\right\}\text{∪}\left\{\frac{5}{2};+\infty\right\}\)
c) \(f\left(x\right)=x^2+12x+36\text{ có }\Delta=0\Rightarrow\text{Nghiệm là: }-6\)
Ta có bảng xét dấu:
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\ne-6\)
\(f\left(x\right)=0\Leftrightarrow x=-6\)
Ta có thể phân tích như sau: \(f\left(x\right)=\left(x+6\right)^2\ge0;\forall x\inℝ\)
d) \(f\left(x\right)=\left(2x-3\right)\left(x+5\right)\text{ có hai nghiệm phân biệt: }\orbr{\begin{cases}x_1=\frac{3}{2}\\x_2=-5\end{cases}}\)
Ta có bảng xét dấu:
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left\{-\infty;-5\right\}\text{∪}\left\{\frac{3}{2};+\infty\right\}\)
\(f\left(x\right)=0\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{3}{2}\end{cases}}\)
\(f\left(x\right)< 0\Leftrightarrow x\in\left\{-5;\frac{3}{2}\right\}\)
TT
0
17 tháng 2 2022
b: \(\Delta=2^2-4\cdot1\cdot1=0\)
Do đó: Tam thức này dương khi x khác -1; bằng 0 khi x=-1
a: \(\Delta=3^2-4\cdot\left(-5\right)\cdot\left(-1\right)=9-20=-11< 0\)
Do đó: Tam thức này luôn âm với mọi x
c: \(\Delta=1^2-4\cdot1\cdot\left(-2\right)=9\)
Do đó: Tam thức này âm khi -2<x<1
Bằng 0 khi x=-2 hoặc x=1
Dương khi x<-2 hoặc x>1
PT
1
CM
7 tháng 4 2017
f(x) = x2 – 5x +4
f(4)= 0; f(2) = -2 < 0; f(-1)= 10 > 0; f(0) = 4 > 0
KT
0
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \(f\left( x \right) = 6{x^2} + 41x + 44\) có \(\Delta = 625 > 0\), có hai nghiệm phân biệt là \({x_1} = - \frac{{11}}{2},{x_2} = - \frac{4}{3}\) và có \(a = 6 > 0\)
Ta có bảng xét dấu \(f\left( x \right)\)như sau:
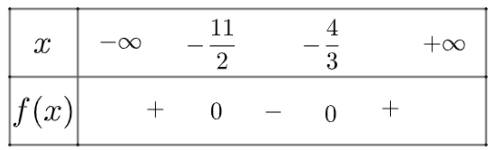
Vậy \(f\left( x \right)\) dương trong khoảng \(\left( { - \infty ; - \frac{{11}}{2}} \right) \cup \left( { - \frac{4}{3}; + \infty } \right)\) và âm trong khoảng \(\left( { - \frac{{11}}{2}; - \frac{4}{3}} \right)\)
b) \(g\left( x \right) = - 3{x^2} + x - 1\) có \(\Delta = - 11 < 0\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau
Vậy \(g\left( x \right)\)luôn âm với mọi \(x \in \mathbb{R}\)
c) \(h\left( x \right) = 9{x^2} + 12x + 4\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = - \frac{2}{3}\) và có \(a = 9 > 0\)
Ta có bảng xét dấu của \(h\left( x \right)\) như sau:
Vậy \(h\left( x \right)\) luôn dương khi \(x \ne - \frac{2}{3}\)
7 tháng 4 2017
a)
\(\Delta=9-20=-11\) vô nghiêm
=> A luôn dương (+) với mọi x thuộc R
b) {a-b+c=0}
B= 0 khi x= -1 hoặc x= 5/2
B>0 khi -1<x<5/2
B<0 khi x<-1 hoặc x>/52
c) x^2 +12x+36 =(x+6)^2
C = 0 khi x =-6
C > 0 mọi x khác -6
d)
D = 0 khi x =3/2 hoặc x=-5
D> 0 khi x<-5 hoặc x>3/2
D<0 khi -5<x<3/2
CM
10 tháng 3 2018
Đáp án: A
Từ bảng xét dấu ta thấy phương trình f(x) = 0 có 2 nghiệm là -3 và 2. Do đó, ta loại được đáp án C và D
Dựa vào bảng xét dấu, f(x) > 0 trong khoảng (-3;2) do đó hệ số a < 0
CY
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2021
\(g\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{5}{2}\end{matrix}\right.\)
\(\Rightarrow g\left(x\right)>0\) khi \(-1< x< \dfrac{5}{2}\) ; \(g\left(x\right)< 0\) khi \(\left[{}\begin{matrix}x< -1\\x>\dfrac{5}{2}\end{matrix}\right.\)
\(h\left(x\right)=\left(x+6\right)^2\Rightarrow h\left(x\right)>0\) ; \(\forall x\ne-6\)
Tam thức f(x) = x2 + 12x + 36 có một nghiệm là x = –6, hệ số a = 1 > 0.
Ta có bảng xét dấu:
Vậy f(x) > 0 với ∀ x ≠ –6
f(x) = 0 khi x = –6