Tìm các giá trị x thỏa mãn điều kiện của bất phương trình sau: 1 x 2 - 4 ≤ 2 x x 2 - 4 x + 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


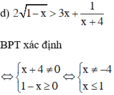
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = (–∞; 1] \ {–4}.

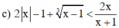
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}

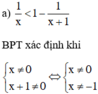
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}

\(\Delta=\left(4m+1\right)^2-8\left(m-4\right)=16m^2+33>0;\forall m\)
Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-4m-1\\x_1x_2=2m-8\end{matrix}\right.\)
a. Kết hợp hệ thức Viet và đề bài: \(\left\{{}\begin{matrix}x_1+x_2=-4m-1\\x_2-x_1=17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=-2m-9\\x_2=-2m+8\end{matrix}\right.\)
Thế vào \(x_1x_2=2m-8\)
\(\Rightarrow\left(-2m-9\right)\left(-2m+8\right)=2m-8\)
\(\Leftrightarrow m^2-9m+20=0\Rightarrow\left[{}\begin{matrix}m=4\\m=5\end{matrix}\right.\)
b.
\(A=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(A=\left(4m+1\right)^2-8\left(m-4\right)\)
\(A=16m^2+33\ge33\)
\(A_{min}=33\) khi \(m=0\)
c.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-4m-1\\x_1x_2=2m-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-4m-1\\2x_1x_2=4m-16\end{matrix}\right.\)
Cộng vế với vế:
\(x_1+x_2+2x_1x_2=-17\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m

Δ=(2n+2)^2-4(n^2+2)
=4n^2+8n+4-4n^2-8
=8n-4
Để phương trình có hai nghiệm phân biệt thì 8n-4>0
=>n>1/2
x1^3+x2^3=1
=>(x1+x2)^3-3x1x2(x1+x2)=1
=>(2n+2)^3-3(n^2+2)(2n+2)=1
=>8n^3+24n^2+24n+8-3(2n^3+2n^2+4n+4)=1
=>8n^3+24n^2+24n+8-6n^3-6n^2-12n-12-1=0
=>2n^3+18n^2+12n-5=0
=>\(n\in\varnothing\)
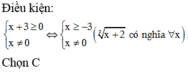
BPT xác định khi
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–2; 1; 2; 3}