Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

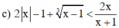
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}

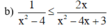
BPT xác định khi
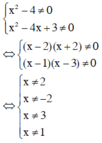
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–2; 1; 2; 3}

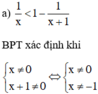
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}

BPT \(x^2-2mx+m^2-m+3\le0\) có tập nghiệm S đã cho nên \(x_1;x_2\) là nghiệm:
\(x^2-2mx+m^2-m+3=0\) với \(\Delta=m^2-\left(m^2-m+3\right)=m-3\ge0\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-m+3\end{matrix}\right.\)
Mặt khác, do \(x_1\) là nghiệm nên: \(x_1^2=2mx_1-m^2+m-3\)
Thay vào bài toán:
\(\sqrt{2mx_1-m^2+m-3+2mx_2+m^2-m+3}=\left|m-9\right|\)
\(\Leftrightarrow\sqrt{2m\left(x_1+x_2\right)}=\left|m-9\right|\)
\(\Leftrightarrow\sqrt{4m^2}=\left|m-9\right|\)
\(\Leftrightarrow4m^2=m^2-18m+81\Rightarrow\left[{}\begin{matrix}m=3\\m=-9\left(loại\right)\end{matrix}\right.\)

Chọn D.
Với m = 1 hệ bất phương trình trở thành:
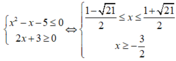
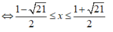
Vậy tập nghiệm hệ bất phương trình là
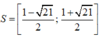

\(\Delta'=\left(m-1\right)^2+m^3-\left(m+1\right)^2=m^3-4m\ge0\) \(\Rightarrow\left[{}\begin{matrix}m\ge2\\-2\le m\le0\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m^3+\left(m+1\right)^2\end{matrix}\right.\)
Do \(x_1+x_2\le4\Rightarrow m-1\le2\Rightarrow m\le3\)
\(\Rightarrow\left[{}\begin{matrix}2\le m\le3\\-2\le m\le0\end{matrix}\right.\)
\(P=x_1^3+x_2^3+3x_1x_2\left(x_1+x_2\right)+8x_1x_2\)
\(=\left(x_1+x_2\right)^3+8x_1x_2\)
\(=8\left(m-1\right)^3+8\left[-m^3+\left(m+1\right)^2\right]\)
\(=8\left(5m-2m^2\right)\)
\(P=8\left(5m-2m^2-2+2\right)=16-8\left(m-2\right)\left(2m-1\right)\le16\)
\(P_{max}=16\) khi \(m=2\)
\(P=8\left(5m-2m^2+18-18\right)=8\left(9-2m\right)\left(m+2\right)-144\ge-144\)
\(P_{min}=-144\) khi \(m=-2\)

Chọn D
Ta có: ( 2m+1) x+ m-5 ≥ 0 tương đương: ( 2m+ 1) x≥ 5- m (*)
+ TH1: Với m> -1/2 , bất phương trình (*) trở thành: 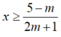
Tập nghiệm của bất phương trình là 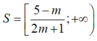
Để bất phương trình đã cho nghiệm đúng với 0< x< 1 thì 
Hay 
+ TH2: m= -1/ 2, bất phương trình (*) trở thành: 0x ≥ 5+ 1/2
Bất phương trình vô nghiệm. Nên không có m thỏa mãn
+ TH3: Với m< -1/ 2 , bất phương trình (*) trở thành: 
Tập nghiệm của bất phương trình là 
Để bất phương trình đã cho nghiệm đúng với 0< x < 1thì 
Hay 
Kết hợp điều kiện m< -1/ 2 nên không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với mọi x: 0< x< 1

`[2-x]/[x+3] > x+1` `ĐK: x \ne -3`
`=>` Loại đ/á `\bb A`
Thay `x=-1` vào bất ptr có: `1,5 > 0` (Luôn đúng) `->\bb B` t/m
Thay `x=2` vào bất ptr có: `0 > 3` (Vô lí) `->\bb C` loại
Thay `x=0` vào bất ptr có: `2/3 > 1` (Vô lí) `->\bb D` loại
______________________________________________________
`=>` Chọn `\bb B`
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = (–∞; 1] \ {–4}.