Cho tỉ lệ thức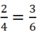 
Hãy so sánh các tỉ số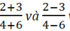 
với các tỉ số trong tỉ lệ thức đã cho.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PT
1
CM
Cao Minh Tâm
16 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
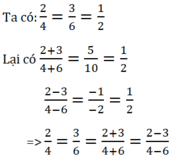
Ta có tỉ thức : \(\dfrac{3}{7} = \dfrac{9}{{21}}\)
Xét \(\dfrac{{3 + 9}}{{7 + 21}}\) = \(\dfrac{{12}}{{28}}\) = \( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 4 )
Xét \(\dfrac{{3 - 9}}{{7 - 21}}\) = \(\dfrac{{ - 6}}{{ - 14}}\)\( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 2 )
Sau khi thực hiện tính các tỉ số ta thấy các kết quả sau khi tối giản của tỉ số bằng với các tỉ só trong tỉ lệ thức đã cho.
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Ta có:
\(\begin{array}{l}\dfrac{{2 + 6}}{{3 + 9}} =\dfrac{{2 - 6}}{{3 - 9}} \end{array}\) (cùng \(= \dfrac{2}{3}\))
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) Ta có:
\(\begin{array}{l}\frac{6}{{10}} = \frac{{6:2}}{{10:2}} = \frac{3}{5};\\\frac{9}{{15}} = \frac{{9:3}}{{15:3}} = \frac{3}{5}\end{array}\)
\(\begin{array}{l}\frac{{6 + 9}}{{10 + 15}} = \frac{{15}}{{25}} = \frac{{15:5}}{{25:5}} = \frac{3}{5};\\\frac{{6 - 9}}{{10 - 15}} = \frac{{ - 3}}{{ - 5}} = \frac{3}{5}\end{array}\)
Ta được: \(\frac{{6 + 9}}{{10 + 15}} = \frac{{6 - 9}}{{10 - 15}} = \frac{6}{{10}} = \frac{9}{{15}}\)
b) - Vì \(k = \frac{a}{b} \Rightarrow a = k.b\)
Vì \(k = \frac{c}{d} \Rightarrow c = k.d\)
- Ta có:
\(\begin{array}{l}\frac{{a + c}}{{b + d}} = \frac{{k.b + k.d}}{{b + d}} = \frac{{k.(b + d)}}{{b + d}} = k;\\\frac{{a - c}}{{b - d}} = \frac{{k.b - k.d}}{{b - d}} = \frac{{k.(b - d)}}{{b - d}} = k\end{array}\)
- Như vậy, \(\frac{{a + c}}{{b + d}}\) =\(\frac{{a - c}}{{b - d}}\) = \(\frac{a}{b}\) =\(\frac{c}{d}\)( = k)
16 tháng 9 2023
a: \(\dfrac{6+9}{10+15}=\dfrac{15}{25}=\dfrac{3}{5};\dfrac{6-9}{10-15}=\dfrac{-3}{-5}=\dfrac{3}{5}\)
=>Bằng nhau
b: a/b=c/d=k
=>a=bk; c=dk
\(\dfrac{a+c}{b+d}=\dfrac{bk+dk}{b+d}=k;\dfrac{a-c}{b-d}=\dfrac{bk-dk}{b-d}=k\)
=>\(\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}=\dfrac{a}{b}=\dfrac{c}{d}\)
6 tháng 10 2016
Giải:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)
Vậy \(\frac{2+3}{4+6}=\frac{2-3}{4-6}\)
KN
với các tỉ số trong tỉ lệ thức đã cho.
1
21 tháng 9 2018
\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}\)
\(\frac{2}{4}=\frac{3}{6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) Vì hai đại lượng x,y tỉ lệ thuận, liên hệ với nhau bởi công thức y = 3.x nên hệ số tỉ lệ k = 3
b) Ta có:
\(\begin{array}{l}\frac{{{y_1}}}{{{x_1}}} = \frac{9}{3} = 3;\frac{{{y_2}}}{{{x_2}}} = \frac{{15}}{5} = 3;\frac{{{y_3}}}{{{x_3}}} = \frac{{21}}{7} = 3\\ \Rightarrow \frac{{{y_1}}}{{{x_1}}} = \frac{{{y_2}}}{{{x_2}}} = \frac{{{y_3}}}{{{x_3}}}\end{array}\)
c) Ta có:
\(\begin{array}{l}\frac{{{x_1}}}{{{x_2}}} = \frac{3}{5};\frac{{{y_1}}}{{{y_2}}} = \frac{9}{{15}} = \frac{3}{5} \Rightarrow \frac{{{x_1}}}{{{x_2}}} = \frac{{{y_1}}}{{{y_2}}}\\\frac{{{x_1}}}{{{x_3}}} = \frac{3}{7};\frac{{{y_1}}}{{{y_3}}} = \frac{9}{{21}} = \frac{3}{7} \Rightarrow \frac{{{x_1}}}{{{x_3}}} = \frac{{{y_1}}}{{{y_3}}}\end{array}\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) Hệ số tỉ lệ a = x1.y1 = 20. 9 =180
b) Ta có: y= \(\frac{{180}}{x}\)
Khi x2 = 18 thì y2 = \(\frac{{180}}{{{x_2}}} = \frac{{180}}{{18}} = 10\)
Khi x3 = 15 thì y3 = \(\frac{{180}}{{{x_3}}} = \frac{{180}}{{15}} = 12\)
Khi x4 = 18 thì y4 = \(\frac{{180}}{{{x_4}}} = \frac{{180}}{5} = 36\)
c) Tích x1.y1 = 20. 9 =180
x2.y2 = 18.10 =180
x3.y3 = 15.12 =180
x4.y4 = 5.36 =180
Vậy x1y1 = x2y2 = x3y3 = x4y4 =180
d) Ta có:
\(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{20}}{{18}}\)=\(\frac{{10}}{9}\) ; \(\frac{{{y_2}}}{{{y_1}}}\)= \(\frac{{10}}{9}\)
\(\frac{{{x_1}}}{{{x_3}}}\) = \(\frac{{20}}{{15}}\)=\(\frac{4}{3}\) ; \(\frac{{{y_3}}}{{{y_1}}}\) = \(\frac{{12}}{9}\) = \(\frac{4}{3}\)
\(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{15}}{5}\) = 3; \(\frac{{{y_4}}}{{{y_3}}}\)= \(\frac{{36}}{{12}}\) = 3
Vậy \(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{x_3}}}\)= \(\frac{{{y_3}}}{{{y_1}}}\); \(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{{y_4}}}{{{y_3}}}\)