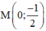Chứng minh rằng khi k thay đổi, các đường thẳng (k + 1)x – 2y = 1 luôn đi qua một điểm cố định. Tìm điểm cố định đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 2 2019
Giả sử đường thẳng (k + 1)x – 2y = 1 đi qua điểm cố định M ( x 0 ; y 0 )
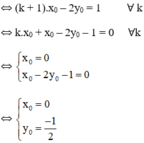
Vậy điểm cố định mà đường thẳng (k + 1)x – 2y = 1 đi qua là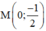 
NT
chứng minh rằng khi k thay đổi các đường thẳng (k+1)x-2y=1 luôn đi qua một điểm cố định. tìm điển đó
1
NN
23 tháng 4 2017
Giải:
Trong phương trình biểu diễn các đường thẳng \(\left(k+1\right)x-2y=1\) ta nhận thấy:
Khi \(x=0\) thì:
Điều này chứng tỏ rằng các đường thẳng có phương trình:
\(\left(k+1\right)x-2y=1\) luôn luôn đi qua điểm cố định I có tọa độ \(\left(0;\frac{1}{2}\right)\forall k\in R\)
25 tháng 4 2017
Hướng dẫn trả lời:
Trong phương trình biểu diễn các đường thẳng (k + 1)x – 2y = 1, ta nhận thấy: Khi x = 0 thì
Điều này chứng tỏ rằng các đường thẳng có phương trình:
(k + 1)x – 2y = 1 luôn luôn đi qua điểm cố định I có tọa độ (0;−12)∀k∈R
CM
16 tháng 6 2017
Gọi điểm cố định mà các đường thẳng (d) đều đi qua P( x o , y o ).
Ta có:
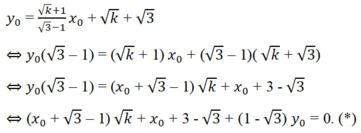
Phương trình (*) nghiệm đúng với mọi giá trị không âm của k , do đó ta có:
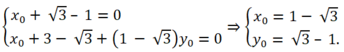
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P(1- 3 ; 3 – 1).
DQ
0
CM
4 tháng 6 2019
Với k ≥ 0 ta có:
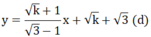
Giả sử ( x 0 ; y 0 ) là điểm cố định mà (d) luôn đi qua
Khi đó ta có:
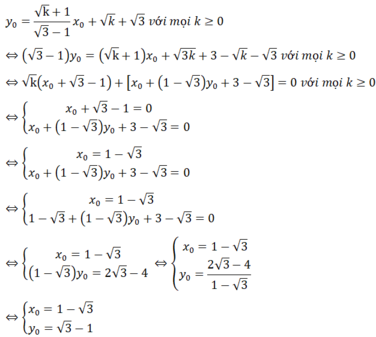
Vậy điểm cố định mà (d) luôn đi qua với mọi k ≥ 0 là (1- 3 ; 3 -1)
VA
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
5 tháng 12 2023
Giả sử \(A\left(x_0;y_0\right)\) là điểm cố định mà \(y=\left(m-2\right)x+3m-1\) luôn đi qua \(\forall m\)
\(\Rightarrow y_0=\left(m-2\right)x_0+3m-1\)
\(\Leftrightarrow y_0-mx_0+2x_0-3m+1=0\)
\(\Leftrightarrow m\left(x_0+3\right)-y_0-2x_0-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+3=0\\-y_0-2x_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-3\\y_0=-5\end{matrix}\right.\)
Vậy với mọi m đường thẳng đã cho luôn đi qua điểm cố định có tọa độ (-3; -5)
5 tháng 12 2023
Gọi điểm cố định đó là \(M\left(x_0;y_0\right)\)
Theo đề bài, ta có:
\(y_0=\left(m-2\right)x_0+3m-1\) với mọi m
\(\Leftrightarrow\left(x_0+3\right)m-2x_0-y_0-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0=-3\\2x_0+y_0+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0=-3\\y_0=5\end{matrix}\right.\)
Vậy đường thẳng đã cho luôn đi qua điểm \(M\left(-3;5\right)\) cố định.
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
Giả sử d đi qua điểm cố định có tọa độ \(\left(x_0;y_0\right)\)
\(\Rightarrow\) Với mọi m ta có:
\(y_0=\left(m+1\right)x_0-3m+4\)
\(\Leftrightarrow m\left(x_0-3\right)+x_0-y_0+4=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0-3=0\\x_0-y_0+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0=3\\y_0=7\end{matrix}\right.\)
Vậy với mọi m thì đường thẳng luôn đi qua điểm cố định có tọa độ \(\left(3;7\right)\)
CM
7 tháng 7 2018
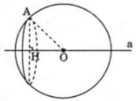
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.
Giả sử đường thẳng (k + 1)x – 2y = 1 đi qua điểm cố định M(x0; y0)
Vậy điểm cố định mà đường thẳng (k + 1)x – 2y = 1 đi qua là