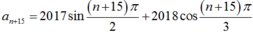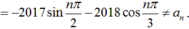Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Ta có :
P = sin(π + α).cos(π - α) = -sin α.(-cos α) = sin α.cos α.
Và 
= cos α.(-sin α) = -sin α.cos α.
Do đó; P + Q = 0.
Chọn B.
Phương pháp:
Cách giải: Ta có:
x n + 1 = x n 2 ( 2 n + 1 ) x n + 1
⇔ 1 x n + 1 = 2 ( 2 n + 1 ) + 1 x n
Đặt u n = 1 x n
ta có: u n + 1 = 2 ( 2 n + 1 ) + u n
Vậy u 100 = 2 ( 2 . 99 + 1 ) + 2 ( 2 . 98 + 1 ) + . . . 2 ( 2 . 1 + 1 ) + 3 2
⇒ = 39999 2
Vậy x 100 = 39999 2
ta thấy 1 số chính phương không bao giờ có đuôi là 2;3;7;8
Mà nếu mệnh đề (2) đúng thì n+8=...2 => mệnh đề (1) sai và n-1=...3 => mệnh đề (3) sai
Nhưng chỉ có 1 mệnh đề sai nên chỉ có mệnh đề (2) là thỏa mãn
Vậy n+8 và n+1 là số chính phương
\(\Rightarrow\left(n+8\right)-\left(n-1\right)=9\)
\(\Leftrightarrow\left(n+8\right)^2-\left(n-1\right)^2=9^2\)
\(\Leftrightarrow\left[\left(n+8\right)-\left(n-1\right)\right]\left[\left(n+8\right)+\left(n-1\right)\right]=9^2\)
\(\Leftrightarrow9\left(2n+7\right)=9^2\)
\(\Leftrightarrow2n-7=9\)
\(\Leftrightarrow n=8\)
Vậy n=8 thì mới thỏa mãn mệnh đề (1) và (3)
Mệnh đề: "Với mọi số nguyên n không chia hết cho 3, n 2 − 1 chia hết cho 3".
Mệnh đề phủ định của mệnh đề trên là "Tồn tại số nguyên n không chia hết cho 3, n 2 − 1 không chia hết cho 3".
Mệnh đề phủ định của mệnh đề " ∀ x ∈ X ; P ( x ) " là " ∃ x ∈ X ; P ( x ) ¯ "
Đáp án A
Đáp án A
y = − x 3 + 3 x 2 − 2017 ⇒ y ' = − 3 x 2 + 6 x y ' = 0 ⇒ x = 0 x = 2
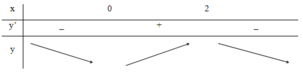
Ta thấy, hàm số nghịch biến trên khoảng (-∞;0) và (2;+∞)
Tại điểm x = - π hàm số không xác định nên hàm số gián đoạn.
Ta có
lim x → 0 - f x = lim x → 0 - 2 sin x x = 2 lim x → 0 + f x = lim x → 0 + x + 2 = 2 = f 0
Do lim x → 0 + f(x) = lim x → 0 - f(x) = f(0) nên hàm số liên tục tại điểm x = 0.
Vậy hàm số chỉ gián đoạn tại điểm x = - π
Đáp án A
Chọn A.
Ta có a1 + a2 + … + an = Sn = n3 và có a1 + a2 + … + an-1 = Sn-1 = (n – 1)3.
Suy ra an = Sn – Sn-1 = n3 – (n – 1)3 = 3n2 – 3n + 1.
Ta có an = 3n2 – 3n + 1.
và an-1 = 3(n – 1)2 – 3(n – 1) + 1 = 3n2 – 9n + 7.
Do đó an – an-1 = 6n – 1 ≥ 0.
Dấu bằng chỉ xảy ra khi n – 1 = 0 hay n = 1. suy ra dãy số (an) là dãy số tăng.
Chọn C.
Kiểm tra từng phương án đến khi tìm được đáp án đúng.
+ Ta có
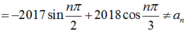
+ Ta có
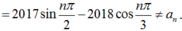
+ Ta có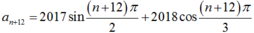
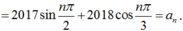
+ Ta có
