Hai lực có độ lớn 3N và 5N hợp với nhau góc 600. Tìm độ lớn của hợp lực.
A. 7 N.
B. 4,4 N.
C. 8 N.
D. 5,8 N.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Ta có lực tổng hợp thỏa mãn tính chất
F min ≤ F ≤ F max ⇒ F 1 − F 2 ≤ F ≤ F 1 + F 2 ⇒ 1 N ≤ F ≤ 7 N
Vậy hợp lực của chúng có thể là 5N
b. Ta có
F 2 = F 1 2 + F 2 2 + 2 F 1 F 2 cos α ⇒ 5 2 = 3 2 + 4 2 + 2.3.4. cos α ⇒ α = 90 0

Ta thử đáp án là cách nhanh nhất nhé!
Thay vào công thức:
\(F=\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\alpha}\)
Lần lượt thay ta đc đáp án B thỏa man nhé:
\(F=\sqrt{16^2+12^2+2\cdot16\cdot12\cdot cos90^o}=20N\)
Chọn B

a:
Gọi hai lực đồng quy đề bài cho lần lượt là \(\overrightarrow{F_1};\overrightarrow{F_2}\)
Gọi hợp lực của \(\overrightarrow{F_1};\overrightarrow{F_2}\) là \(\overrightarrow{F}\)
Do đó, ta có: \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
=>\(\left|\overrightarrow{F}\right|=\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)}\)
=>\(F=\sqrt{18^2+24^2+2\cdot18\cdot24\cdot cos25}\simeq41,02\left(N\right)\)
b: \(F=31N\)
=>\(\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)}=31\)
=>\(900+2\cdot18\cdot24\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=961\)
=>\(864\cdot cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=61\)
=>\(cos\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)=\dfrac{61}{864}\)
=>\(\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)\simeq86^0\)

Chọn B.
Ta tổng hợp theo phương pháp số phức:
+ Chọn trục trùng véc tơ F 1 → làm trục chuẩn thì F 2 → sớm hơn F 1 → một góc 600 và F 3 → sớm hơn F 1 → một góc 1200.
+ Tổng phức:
![]()

Trong phép tổng hợp hai lực thì hai lực thành phần cùng với hợp lực tạo thành một hình tam giác. Độ lớn của các lực biểu diễn bằng độ dài của các cạnh tam giác đó.
Từ định lí hàm số cosin đối với tam giác, áp dụng cho trường hợp này ta có góc giữa hai lực đồng quy xác định bởi:
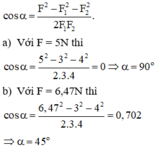
Đáp án A.