Giả sử f là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?
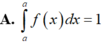

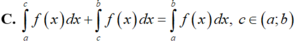
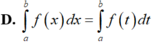
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phương pháp : Dựa vào các tính chất tích phân đã được học để nhận biết.
Cách giải : Dễ thấy A đúng.

+) Đáp án A:
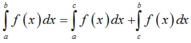
đáp án A đúng.
+) Đáp án C:
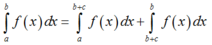
đáp án C đúng.
+) Đáp án D:
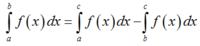
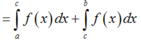
đáp án D đúng.
Chọn B.

Đáp án C
Từ đồ thị hàm số g = f’(x) ta thấy: hàm số f’(x) = 0 tại 2 điểm phân biệt x = -2 và x = 1
Mặt khác, tại x = 1 thì f’(x) đổi dấu từ dương sang âm, do đó hàm số y = f(x) đạt cực đại tại x = 1

Đáp án C
Từ đồ thị hàm số g = f’(x) ta thấy: hàm số f’(x) = 0 tại 2 điểm phân biệt x = -2 và x = 1
Mặt khác, tại x = 1 thì f’(x) đổi dấu từ dương sang âm, do đó hàm số y = f(x) đạt cực đại tại x = 1

Theo tính chất tích phân ta có:
+ ) ∫ a b f ( x ) d x + ∫ b c f ( x ) d x + ∫ c a f ( x ) d x
∫ c a f ( x ) d x + ∫ c a f ( x ) d x = ∫ a a f ( x ) d x = 0
Đáp án A đúng.
+ ) ∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x
với
c
∈
ℝ
.Đáp án B đúng.
+ ) ∫ a b ( f ( x ) - g ( x ) ) d x + ∫ a b g ( x )
= ∫ b a f ( x ) d x - ∫ a b g ( x ) d x + ∫ a b g ( x ) d x = ∫ a b f ( x ) d x
Đáp án D đúng.
Đáp án C sai.
Chọn đáp án C.
Chọn A
Ta có: ∫ a a f x d x = F a - F a = 0 .