Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 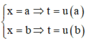
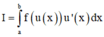


+) Đáp án A:
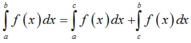
đáp án A đúng.
+) Đáp án C:
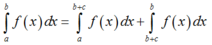
đáp án C đúng.
+) Đáp án D:
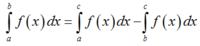
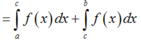
đáp án D đúng.
Chọn B.

Theo tính chất tích phân ta có:
+ ) ∫ a b f ( x ) d x + ∫ b c f ( x ) d x + ∫ c a f ( x ) d x
∫ c a f ( x ) d x + ∫ c a f ( x ) d x = ∫ a a f ( x ) d x = 0
Đáp án A đúng.
+ ) ∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x
với
c
∈
ℝ
.Đáp án B đúng.
+ ) ∫ a b ( f ( x ) - g ( x ) ) d x + ∫ a b g ( x )
= ∫ b a f ( x ) d x - ∫ a b g ( x ) d x + ∫ a b g ( x ) d x = ∫ a b f ( x ) d x
Đáp án D đúng.
Đáp án C sai.
Chọn đáp án C.
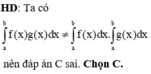
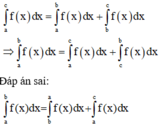
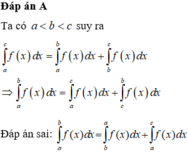
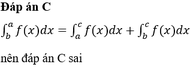
Chọn B