Cho tam giác ABC, hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC
b) Chứng minh AB.AF = AC.AE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 12 2017
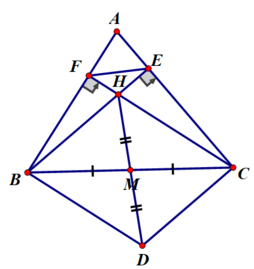
a) Xét tứ giác BFEC có:
∠(BFC) = ∠(BEC) = 90 0 (gt)
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BFEC nội tiếp được đường tròn
CM
19 tháng 11 2019
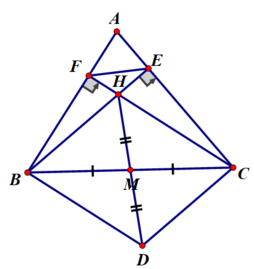
c) Xét tứ giác BHCD có:
M là trung điểm của 2 đường chéo HD và BC
⇒ Tứ giác BHCD là hình bình hành
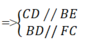
Mà BE ⊥ AC ; FC ⊥ AB
⇒ CD ⊥ AC ; DB ⊥ AB
Xét tứ giác ABDC có:
∠(ABD) = ∠(ACD) = 90 0
∠(ABD ) + ∠(ACD) = 180 0
⇒ Tứ giác ABDC nội tiếp được đường tròn
TN
17 tháng 3 2021
c)Cm:tứ giác ABDC nt đường tròn
Hình tự vẽ nha
Xét tg HBDC,có:
HM=MD(gt)
BM=MC(gt)
Mà M là gđ của HD và BC
Suy ra:tg HBDC là hbh
Suy ra: BHC=BDC(tc hbh)
Ta có:FHE=BHC(đối đỉnh)
Suy ra:BDC=FHE (1)
Xét tg AFHE,có:
AFH + AEH=90°+90°=180°
Mà 2 góc ở vị trí đối nhau
Suy ra:tg AFHE nội tiếp
Suy ra:FAE +FHE=180° (2)
Từ (1)và(2)suy ra:BAC+BDC=180°
Mà 2 góc ở vị trí đối nhau
Suy ra:tgABDC nội tiếp đường tròn(đpcm)
Mong mn thông cảm, viết góc vào hộ mình nha,cảm ơn
Chúc mn học tốt!
29 tháng 1
b: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
=>BHCD là hình bình hành
=>BH//CD và BD//CH
ta có: BH//CD
BH\(\perp\)AC
Do đó: CD\(\perp\)CA
=>ΔCDA vuông tại C
=>ΔCAD nội tiếp đường tròn đường kính AD(1)
Ta có: BD//CH
CH\(\perp\)AB
Do đó: BD\(\perp\)BA
=>ΔBAD vuông tại B
=>ΔBAD nội tiếp đường tròn đường kính AD(2)
Từ (1) và (2) suy ra B,A,D,C cùng thuộc (O), đường kính AD
Xét (O) có
ΔAID nội tiếp
AD là đường kính
Do đó: ΔAID vuông tại I
=>AI\(\perp\)ID tại I
=>AI\(\perp\)IH tại I
=>ΔAIH vuông tại I
=>I nằm trên đường tròn đường kính AH(3)
ta có: \(\widehat{AFH}=\widehat{AEH}=90^0\)
=>A,F,H,E cùng thuộc đường tròn đường kính AH(4)
Từ (3) và (4) suy ra A,F,I,H,E cùng thuộc một đường tròn
10 tháng 5 2023
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F co
góc A chung
=>ΔAEB đồng dạng với ΔAFC
b: ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
NK
30 tháng 4 2019
a, Xét tgABE và tgACF có:
góc AEB = góc CFA = 90o
góc BAC chung
Từ 2 điều trên => tgABE đồng dạng tgACF (g.g)
=> AB/AC = AE/AF (các cặp cạnh tương ứng)
=> AB.AF = AC.AE
18 tháng 12 2021
a: Xét tứ giác BHCK có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BHCK là hình bình hành
18 tháng 12 2021
a: Xét tứ giác BHCK có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BHCK là hình bình hành
24 tháng 10 2021
a: Xét tứ giác BHCK có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BHCK là hình bình hành
b) Xét ΔABF và ΔACE có:
∠(BEA) = ∠(CFA) = 90 0 (gt)
∠(BAC ) chung
⇒ ΔABF ∼ ΔACE (g.g)