Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c. Hãy tính thể tích khối chóp S.ADE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
23 tháng 3 2017
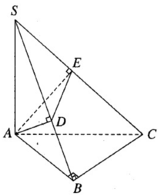
Gọi d là khoảng cách từ E đến mặt phẳng (SAB)
Ta có:
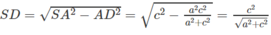
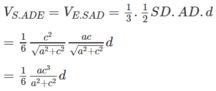
Kết hợp với kết quả trong câu a)
ta suy ra 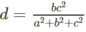

NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)


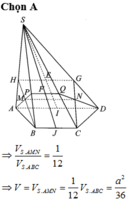
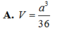
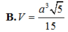

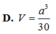
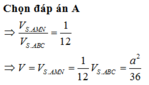
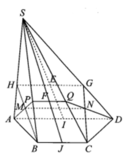

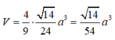

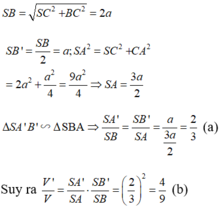
Ta có
Vì AD ⊂ (SAB) nên AD ⊥ BC
Mặt khác AD ⊥ SB nên AD ⊥ (SBC)
Từ đó suy ra AD ⊥ SC
⇒ SC ⊥ DE hay SE ⊥ (ADE)
Trong tam giác vuông SAB ta có: SA.AB = AD.SB
Tương tự, trong tam giác vuông SAC ta có:
Do AD ⊥ (SBC) nên AD ⊥ DE. Từ đó suy ra:
Vậy