Cho năm điểm A, B, C, D, E. Vẽ tất cả các đường thẳng đi qua hai trong năm điểm đó.
Có bao nhiêu đường thẳng nếu ba điểm A, B, C thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2018
a) Mik tính theo công thức :n.(n-1) :2
Số đường thẳng nếu trong năm điểm đã cho không có ba điểm nào thẳng hàng là : \(\frac{5.4}{2}\)= 10 (đường thẳng)
b) Số đường thẳng nếu ba điểm A, B, C thẳng hàng là 8
CM
26 tháng 6 2018
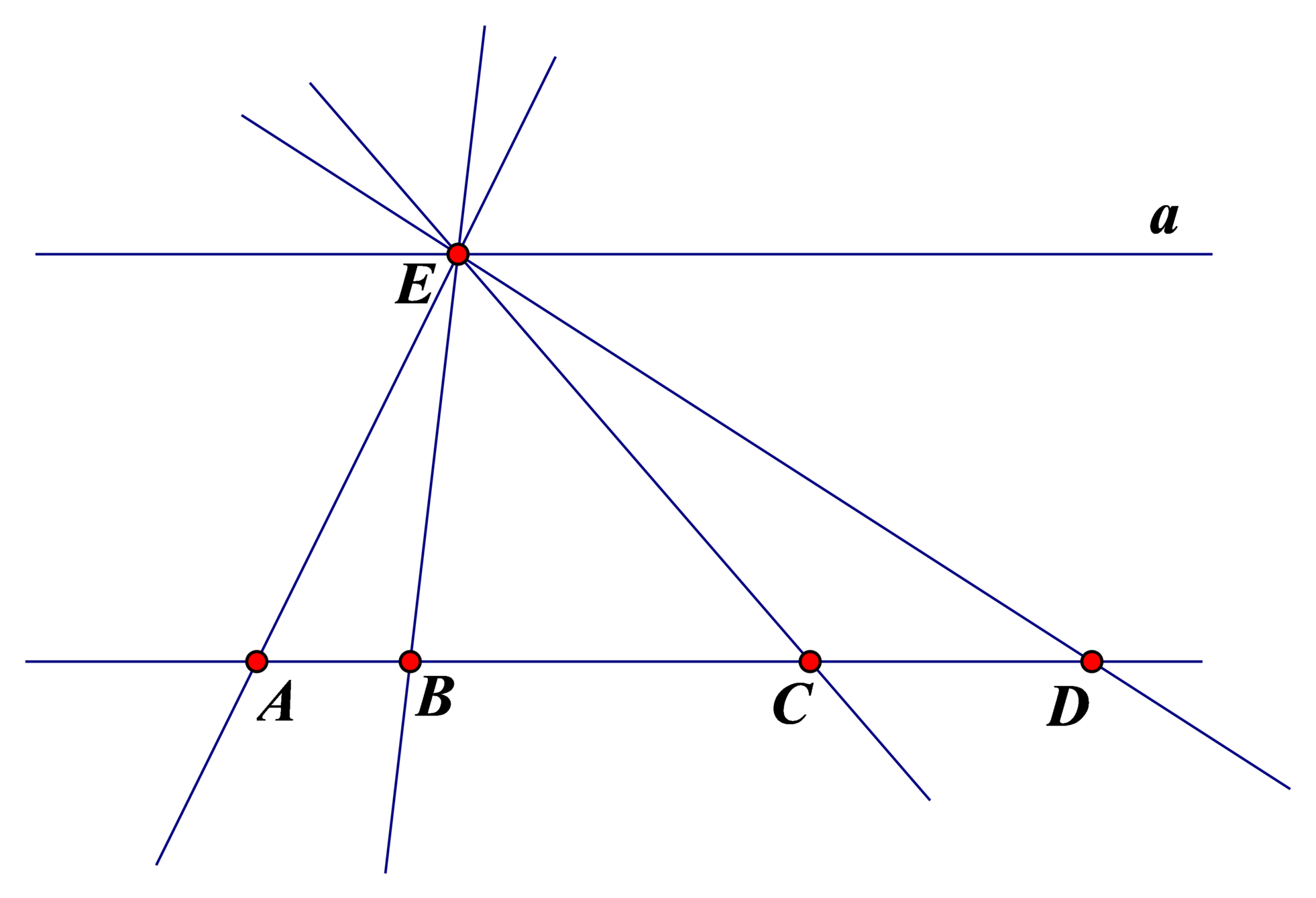
- Có năm đường thảng phân biệt trong hình vẽ, đó là: EA , EB , EC , ED , AB .
- Hai đường thẳng AB và CD trùng nhau; đường thẳng a song song với đường thẳng AB nên cũng song song với đường thẳng CD. Do đó, đường thẳng a không cắt đường thẳng CD.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 9 2023
Cứ hai điểm tạo thành một đoạn thẳng
Có 5 cách chọn điểm thứ nhất, 4 cách chọn điểm thứ hai, số đoạn thẳng được tạo là:
5 x 4 = 20 (đoạn thẳng)
Theo cách tính trên mỗi đoạn thẳng được tính hai lần. Vậy số đoạn thẳng được tạo là: 20 : 2 =10 (đoạn thẳng)
Kết luận:..
5 tháng 7 2023
a: Có \(C^2_5\left(đoạn\right)\)
b: Có 5 đường thẳng đi qua hai điểm bất kì
30 tháng 10 2016
nếu k có 4 điểm thẳng hàng thì ta có:
100x99:2=4950 (đường thẳng)
do có 4 điểm thẳng hàng nên ta chỉ vẽ đc 1 đường thẳng với 4 điểm đó
=> Có tất cả :
4950-(1x4)=4946 ( đường thẳng)
d/s:.....
20 tháng 7 2017
Nếu không có 4 điểm thẳng hàng thì ta có:
100 x 99 : 2 = 4950 ( đường thẳng )
Do có 4 điểm thẳng hàng nên ta chỉ vẽ đươccj 1 đường thẳng với 4 điểm đó.
Có tất cả số đường thẳng là:
4950 - ( 1 x 4 ) = 4946 ( đường thẳng )
Đáp số: 4946 đường thẳng
Cách 1. Vẽ hình và thấy có tất cả là 8
đường thẳng.
Cách 2. Theo ý a), nếu không có ba điểm
nào thẳng hàng thì có 10 đường thẳng.
Với ba điểm A, B, C nếu chúng không thẳng hàng thì có ba đường thẳng, nhưng vì chúng thẳng hàng nên chỉ có một đường thẳng.
Do đó, số đường thẳng phải đếm giảm đi 3 -1 = 2.
Vậy có tất cả 10 - 2 = 8 đường thẳng.