Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2019
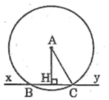
Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm
Mà AH = d = 12cm
Nên suy ra d < R
Vậy (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C
21 tháng 11 2023
a: Kẻ MH vuông góc xy tại H, gọi AB là đường kính của (M)
d(M;xy)=6cm
=>MH=6cm
AB là đường kính của (M)
=>MA=MB=10cm và AB=2*10=20(cm)
Vì MH<MA
nên xy là cát tuyến của (M)
=>(M) cắt xy tại 2 giao điểm
b:
P,Q là 2 giao điểm của (M) với xy
=>MP=MQ=10cm
ΔMPQ cân tại M
mà MH là đường cao
nên H là trung điểm của PQ
ΔMHP vuông tại H
=>\(MP^2=MH^2+HP^2\)
=>\(HP^2=10^2-6^2=64\)
=>HP=8(cm)
H là trung điểm của PQ
=>\(PQ=2\cdot PH=16\left(cm\right)\)
7 tháng 7 2023
a: ΔOMN cân tại O có OD là trung tuyến
nên OD vuông góc NA
góc ODA=góc OBA=90 độ
=>ODBA nội tiếp
b; Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AN*AM
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
19 tháng 9 2018
a/ Xét tg vuông AOH và tg vuông IOK có
\(OI\perp AH;KI\perp AO\Rightarrow\widehat{KIO}=\widehat{HAO}\)
\(\Rightarrow\Delta AOH\) đồng dạng với \(\Delta IOK\)(Hai tg vuông có hai góc nhọn tương ứng bằng nhau) (1)
b/
Từ (1) \(\Rightarrow\frac{OK}{OH}=\frac{OI}{OA}\Rightarrow OH.OI=OK.OA\)
Ta có \(OA\perp BC\)(Hai tiếp tuyến xuất phát từ 1 điểm ngoài đường tròn thì đường thẳng nối điểm đó với tâm vuông góc và chia đôi dây cung tạo bởi hai tiếp điểm)
Xét tg vuông ABO có \(OB^2=OK.OA=3\) không đổi
\(\Rightarrow OH.OI\)không đổi mà OH không đổi => OI không đổi
Mà H; O cố định => I cố định => Khi A chay trên xy thì BC luôn đi qua điểm I cố định
CM
25 tháng 12 2018
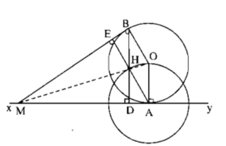
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
Áp dụng định lí Pitago vào tam giác vuông AHC ta có:
A C 2 = A H 2 + H C 2
Suy ra: H C 2 = A C 2 - A H 2 = 13 2 - 12 2 = 25 => HC = 5 (cm)
Ta có: BC = 2.HC = 2.5 = 10 (cm)