Tìm hệ số cuả x 8 trong khai triển đa thức f ( x ) = 1 + x 2 ( 1 - x ) 8
A: 218
B: 232
C: 238
D: tất cả sai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 8 là \(\left(8a^2-\dfrac{1}{2}b\right)^6\) hay \(\left(8a^2-\dfrac{1}{2b}\right)^6\) bạn? (tốt nhất là bạn dùng tính năng gõ công thức toán để đăng đề, hoặc chụp hình gửi đề trực tiếp lên, hiện nay hoc24 đã cho đăng đề bằng hình ảnh)
9.
\(\left(x+8.x^{-2}\right)^9=\sum\limits^9_{k=0}C_9^kx^{9-k}.8^k.x^{-2k}=\sum\limits^9_{k=0}C_9^k8^kx^{9-3k}\)
Số hạng ko chứa x \(\Rightarrow9-3k=0\Rightarrow k=3\)
Số hạng đó là: \(C_9^3.8^3=...\)

\(f\left(x\right)=\sum\limits^3_{i=0}C_3^i\left(x+x^2\right)^i.\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k\left(2x\right)^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}C_3^i.C_i^jx^j.\left(x^2\right)^{i-j}\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k.2^k.x^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}\sum\limits^{15}_{k=0}C_3^iC_i^jC_{15}^k\left(\dfrac{1}{4}\right)^{3-i}.2^k.x^{2i+k-j}\)
Số hạng chứa \(x^{13}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le i\le3\\0\le j\le i\\0\le k\le15\\2i+k-j=13\end{matrix}\right.\)
\(\Rightarrow\left(i;j;k\right)=\left(0;0;13\right);\left(1;0;12\right);\left(1;1;11\right);\left(2;0;11\right);\left(2;1;10\right);\left(2;2;9\right);\left(3;0;10\right);\left(3;1;9\right)\)
\(\left(3;2;8\right);\left(3;3;7\right)\) (quá nhiều)
Hệ số....
Tìm hệ số của số hạng chứa \(x^5\) trong khai triển đa thức \(f\left(x\right)=x\left(1-2x\right)^5\)

Ta có: \(x.\left(C^k_n.a^{n-k}.b^k\right)=x.\left(C^k_5.a^{5-k}.b^k\right)=C^k_5.1^{5-k}.2^k.x^k.x\)
\(=C^k_5.2^k.x^{k+1}\)
Mà ta cần tìm số hạng của x5
\(\Rightarrow k+1=5\Leftrightarrow k=4\)
Vậy số hạng của x5 là: \(C^4_5.2^4=80\)
Ta nhân thêm ''x'' vào số hạng tổng quát vì có ''x'' là nhân tử chung của mỗi số hạng trong khải triển

Chọn B
Ta có a8= C88+C98+C108+C118+C128= 1+9+45+165+495= 715

15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
C18 , c19 là lm sao vậy ạ ? Mk ko hiểu 2 bài này nơi
Lời giải.
Cách 1:
Trong khai triển trên ta thấy bậc của x trong 3 số hạng đầu nhỏ hơn 8, bậc của x trong 4 số hạng cuối lớn hơn 8.
Do đó x8 chỉ có trong số hạng thứ tư, thứ năm với hệ số tương ứng là: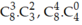 .
.
Vậy hệ số cuả x8 trong khai triển đa thức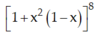 là:
là:
Cách 2: Ta có:
với 0 ≤ k ≤ n ≤ 8.
Số hạng chứa x8 ứng với 2n + k = 8 ⇒ k = 8 -2n là một số chẵn.
Thử trực tiếp ta được k = 0, n =4 và k = 2, n = 3.
Vậy hệ số của x8 là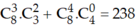
Chọn C.